Développante d'une surface développable

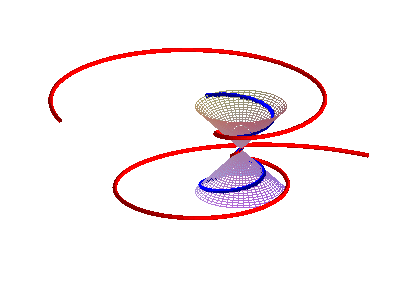
DÉVELOPPANTE D'UNE COURBE, D'UNE SURFACE DÉVELOPPABLE
Involute of a curve, of a developable surface, Evolvente einer Kurve, einer Torse

Développante d'une spirale conique

Notion étudiée par Monge en 1771.

Si M₀ est le point courant de , un point de départ étant choisi pour les abscisses curvilignes, la développante de cette courbe est le lieu des points ;
Paramétrisation cartésienne : .
Rayon de courbure : .

I) Développpantes d'une courbe.

Les développantes d'une courbe sont les trajectoires décrites par les points d'une droite roulant sans glisser sur cette courbe.

Elles forment donc, sur la surface développable des tangentes à , les trajectoires orthogonales à ces tangentes ; et elles forment une classe d'équivalence de courbes parallèles.
Ce sont aussi les courbes dont la courbe de départ est une développée.

Quand on développe la surface sur un plan, les développantes 3D deviennent les développantes 2D de l'image de dans le plan.

Une développante est plane ssi la courbe de départ est une hélice, et alors toutes les développantes sont planes.

II) Développpantes d'une surface développable.

Les développantes d'une surface développable sont les trajectoires d'un point d'un plan roulant sans glisser sur la surface ; ce sont donc les courbes dont la surface de départ est la surface polaire. Elles possèdent un point de rebroussement sur , à tangente orthogonale à ; et elles forment une classe d'équivalence de courbes parallèles.

Lorsque est un cylindre, les développantes sont les développantes des sections planes perpendiculaires à l'axe.

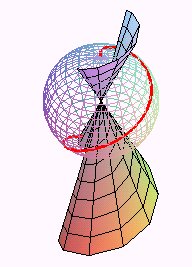
Lorsque est un cône, les développantes sont tracées sur des sphères centrées au sommet du cône : ce sont les lieux d'un point d'un cercle centré au sommet du cône et roulant sans glisser sur une trajectoire orthogonale aux génératrices du cône.

Dans le cas d'un cône de révolution, ce sont donc des hélices sphériques.

Pb : comment obtenir la paramétrisation des développantes de à partir de celle de son arête de rebroussement ????

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres