Hélice senestre

Hélice dextre

Paramétrisation cartésienne : 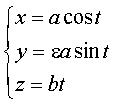. Système d’équations cylindriques : . Abscisse curviligne : , où . Rayon de courbure : , angle de courbure : at / c. Rayon de torsion : , angle de torsion : bt / c. Longueur d’une spire : . Centre de courbure :  (décrit une autre hélice circulaire).

L’hélice circulaire peut être définie comme une hélice tracée sur un cylindre de révolution vertical, ou une loxodromie de ce cylindre (c'est-à-dire, dans les deux cas, une courbe faisant un angle constant avec l’axe du cylindre), ou une géodésique de ce cylindre (autrement dit, une courbe qui devient une droite quand on développe le cylindre) ou enfin un solénoïde d'âme rectiligne.
Caractérisation intrinsèque : courbure et torsion constantes.

Le rayon de l’hélice est a, et son pas est  (c’est la distance entre deux spires consécutives) et l’on appelle parfois b le pas réduit de l’hélice. L’angle de l’hélice est l’angle constant (égal à ) que fait sa tangente avec tout plan orthogonal à Oz. L’hélice est dextre (ou droite) lorsque e = 1 (elle “monte” dans le sens trigonométrique et un observateur placé à l’extérieur la voit, lorsqu'elle est devant, monter de gauche à droite) et senestre (ou gauche) lorsque e = - 1 (elle “monte” dans le sens des aiguilles d’une montre).

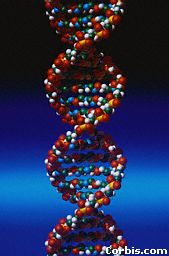
L'ADN s'enroule suivant une double hélice dextre.

Les filetages de vis et de tire-bouchon sont dextres, mais pas ceux des bouteilles de butane.

Les plantes grimpantes s’enroulent suivant des hélices, soit dextres, comme la vigne (d'où l'expression weinwendig en allemand) ou la glycine de Chine, soit senestres, comme le houblon (d'où l'expression hopfenwendig) ou la glycine du Japon (dixit Michel le jardinier sur France-Info).

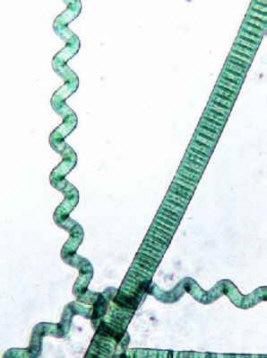
Enfin, on a remarqué au Brésil une espèce de chauve-souris qui s’élèvent invariablement suivant des hélices dextres.

La trajectoire d'une charge dans un champ magnétique uniforme et soumise à la seule force de Laplace est une hélice circulaire d'axe parallèle au champ (ou un cercle si la vitesse est perpendiculaire au champ, une droite si elle est parallèle). Même résultat pour un fil souple inextensible parcouru par un courant continu placé dans le champ (et supposé non soumis à la pesanteur). La forme prise par ce fil a été appelée par Riebke "chaînette électrodynamique", forme qui est donc une hélice circulaire, avec les mêmes cas limites que précédemment.

Démonstration de ce fait :  la relation fondamentale et l'expression de la force de Laplace donnent :   (1) où  est la tension du fil,  le vecteur unitaire tangent,  le champ magnétique et I l'intensité du courant ;  montre que la norme de la tension est constante : T = cte. (1) s'écrit donc  ;  montre que  : la tangente fait un angle constant avec une direction fixe, la courbe est une hélice.  La première formule de Frenet  donne alors avec (2)  : le rayon de courbure est constant. Le rayon de torsion de l'hélice, classiquement donné par  est donc lui aussi constant : la courbe est une hélice circulaire d'axe parallèle aux lignes de champs.

Nota : d'où vient le fait que les systèmes propulseurs à pales des bateaux et des avions s'appellent des hélices ? Du fait que lorsque le bateau avance à vitesse constante, le mouvement de l'hélice par rapport à un repère fixe est un mouvement hélicoïdal, et que tous ses points décrivent des hélices circulaires.

Pour les projections de l’hélice circulaire, voir à trochoïde, à cochléoïde et spirale hyperbolique.
Voir aussi les hélicoïdes, les autres courbes cylindriques, le serpentin (tube d'âme une hélice circulaire), et la révolution de la sinusoïde.
 

Autres belles images : www.mathouriste.eu/Surfaces/quad_archi_hel.html

© Robert FERRÉOL  2018