Paramétrisation cartésienne :  (où d est la distance de M au centre du cercle). Aire d'une arche limitée par la base, dans le cas  :  (obtenue par le théorème de Holditch).

On désigne par trochoïde la courbe décrite par un point lié à un disque de rayon R roulant sans glisser sur une droite (D) ; autrement dit, c'est une roulette d'un mouvement plan sur plan dont la base est une droite et la roulante un cercle.

Pour d < R, la courbe s'appelle aussi cycloïde raccourcie et ressemble à une sinusoïde, ce qu'elle est si l'on néglige le terme  dans x.

Pour d = R, on obtient la cycloïde.

Pour d > R, la courbe s'appelle aussi cycloïde allongée et peut prendre diverses formes, avec de plus en plus de points doubles à mesure que d augmente.
 

Le fait que la cycloïde allongée ait une boucle est à l'origine du paradoxe suivant : Montrer que, dans un train en mouvement, il y a toujours une portion de matière qui se déplace en sens inverse du train (par rapport à la terre). Réponse : le bas du petit rebord des roues.

Le bas de la roue du train avance en sens inverse de la marche....

On peut aussi définir les trochoïdes comme les trajectoires d’un mouvement composé d’un mouvement rectiligne uniforme et d’un mouvement circulaire, de paramétrisation complexe :    ( ) ; ce sont des cycloïdes si  , des cycloïdes raccourcies si , des cycloïdes allongées si  (on peut prendre et  d = r). Le rapport 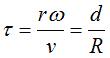 "vitesse de translation sur vitesse de rotation" définit alors entièrement la trochoïde à similitude près, l'allongement augmentant avec . Ci-contre deux cas remarquables où la cycloïde allongée est tangente à elle-même. Le rapport  vaut successivement 4,6....  et 7,8....

Exemples concrets :
 

- vous avancez régulièrement le long d’un tableau tenant une craie à la main d’un mouvement circulaire régulier : vous tracez une trochoïde, en général allongée car vous avancez moins vite que vous ne tournez votre main. - des réflecteurs sur les rayons de votre vélo décrivent des cycloïdes raccourcies. - la pédale de votre vélo décrit, lorsque vous appuyez dessus, des trochoïdes de rapport  où  est le rayon du plateau (roue dentée du pédalier),  est le rayon du pignon (roue dentée de la roue arrière,  est le "ratio"), R le rayon de la roue arrière, et r la longueur du bras de la pédale. Ce nombre étant toujours < 1, c'est une cycloïde raccourcie, le raccourcissement (ou plutôt l'aplatissement) augmentant avec le ratio. - la roue à aube du bateau décrit une trochoïde, allongée, elle, car la prise des pales dans l'eau n'est pas parfaite (la vitesse de l'extrémité de la pale est supérieure à la vitesse du bateau). - Gerstner a montré que la houle prenait une forme trochoïdale, voir wikipedia.

 

Les projections d'une hélice circulaire sur un plan fixé donnent toutes les formes de trochoïdes, éventuellement dilatées ; autrement dit, les trochoïdes sont, à dilatation près, les vues en perspective cavalière, ou bien les ombres, d’un ressort. Lorsque le plan est orthogonal à l'axe de l'hélice, on obtient les trochoïdes non dilatées, la cycloïde étant obtenue pour une direction de projection parallèle à une tangente à l'hélice (théorème de Guillery, 1847).

 

Voir aussi les épi- et hypotrochoïde, la courbe de la mascotte , la courbe de Duporcq, et la surface minimale de Catalan.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2022