Courbe de Duporcq

COURBE DE POURSUITE ORTHOGONALE, COURBE DE DUPORCQ
Orthogonal pursuit curve, Duporcq curve, Querläuferkurve, Duporcqsche Kurve

Courbe étudiée par Duporcq et Mannheim en 1902, Balitran en 1914, Egan en 1919, Masurel en 2014.
Ernest Duporcq (1873-1903) : mathématicien français.
Autre nom : courbe du crabe.
Voir aussi : Walter Wunderlich, Über die Hundekurven mit konstantem Schielwinkel, Monatshefte für Mathematik, 1957, Volume 61, Issue 4, pp 299-303.

Système différentiel : , menant, pour à , soit .

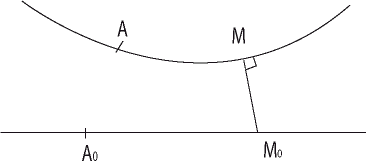
Les courbes de poursuite orthogonale sont les trajectoires d'un mobile M dont le mouvement est dirigé à chaque instant perpendiculairement à la direction d'un autre mobile M₀ (l'initiateur), les deux mobiles ayant des vitesses proportionnelles .
La trajectoire de M₀ étant donnée, celle de M est donc définie dans ce cas par le fait que (MM₀ ) est perpendiculaire en M à sa trajectoire, et l'abscisse curviligne de M est proportionnelle à celle de M₀ :.
On peut imaginer un crabe en M qui marcherait toujours face à l'initiateur M₀ et on pourrait appeler ces courbes "courbes (de poursuite) du crabe".

I) Dans le cas où M₀ a un mouvemnt rectiligne, les trajectoires du "crabe" sont appelées "courbes de Duporcq".
Egan a montré qu'alors le vecteur a le même mouvement qu'un corps en attraction newtonienne, et décrit donc une conique d'excentricité e (d'où l'explication du choix de e pour le rapport des vitesses, au lieu du classique k).

Premier cas : , cas elliptique.

Paramétrisation cartésienne : , , .
Abscisse curviligne : .

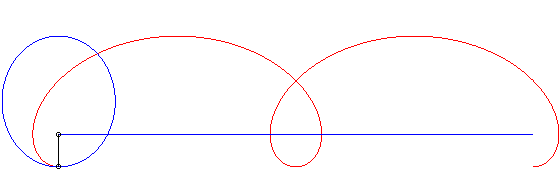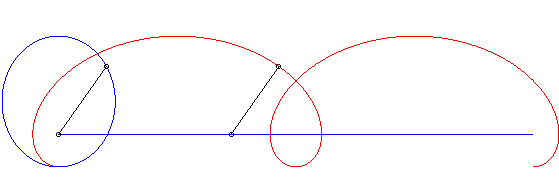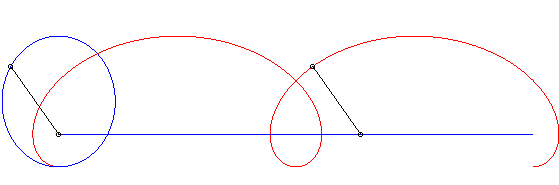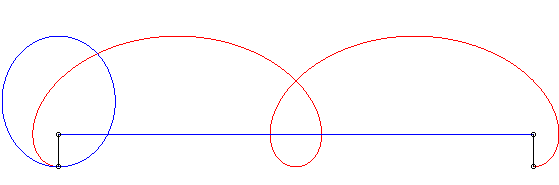
Ci-contre, en bleu, est indiqué le mouvement elliptique du vecteur .
La courbe de Duporcq est dans ce cas l'image par une affinité de rapport d'une cycloïde allongée de rapport .
NOTA 1 : c'est le seul rapport d'affinité qui permet d'intégrer l'abscisse curviligne par fonctions élémentaires.
NOTA 3 : dans les expressions ci-dessus, et comme on le remarque dans l'animation ci-contre, les vitesses de M et de M₀ sont proportionnelles, mais non constantes.

Deuxième cas : , cas parabolique.
a) le crabe et l'initiateur ont, à un instant donné, des vitesses de même sens : le crabe suit évidemment une droite parallèle à celle suivie par l'initiateur.

b) le crabe et l'initiateur ont, à un instant donné, des vitesses de sens contraire.

Paramétrisation cartésienne : ,,
Abscisse curviligne : .

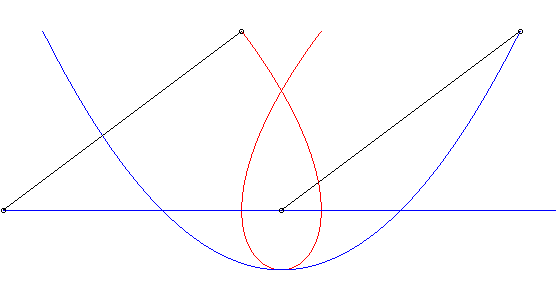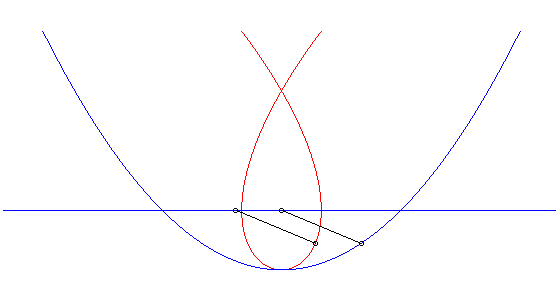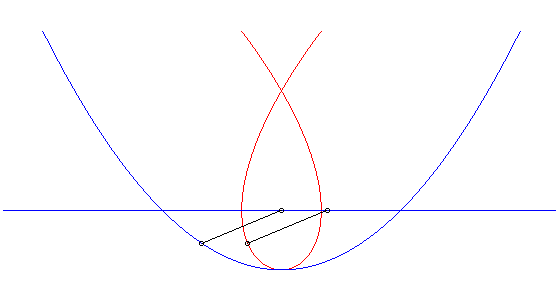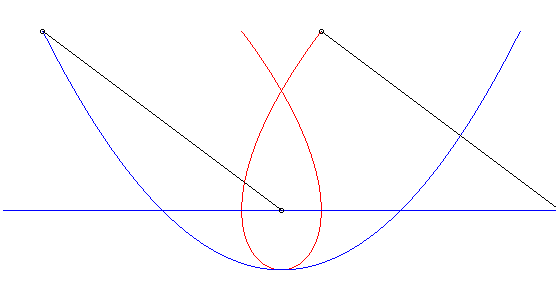
Ci-contre, en bleu, est indiqué le mouvement parabolique du vecteur .
La courbe de Duporcq n'est autre, dans ce cas, que la cubique de Tschirnhausen.
NOTA : le mouvement de M est composé d'un mouvement parabolique et d'un mouvement de translation.

Troisième cas : , cas hyperbolique.

a) le crabe et l'initiateur sont au même point à un instant donné : ils suivent deux droites sécantes.

Ce cas est exclu dans la suite.

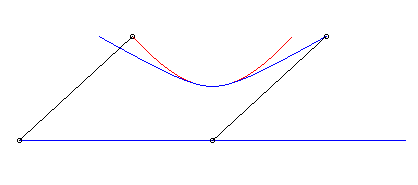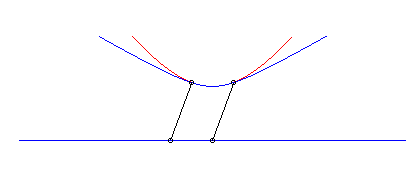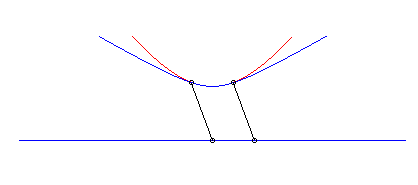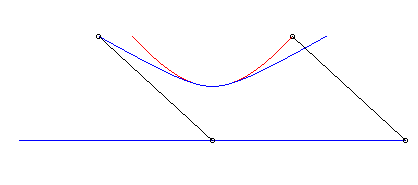
b) le crabe et l'initiateur ont, à un instant donné, des vitesses de même sens :

Paramétrisation cartésienne :, ,

Abscisse curviligne : .
Ci-contre, en bleu, est indiqué le mouvement hyperbolique du vecteur .

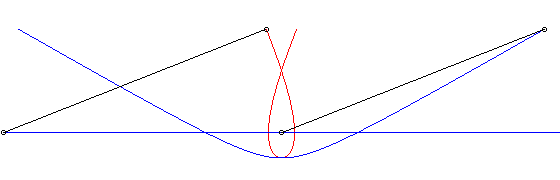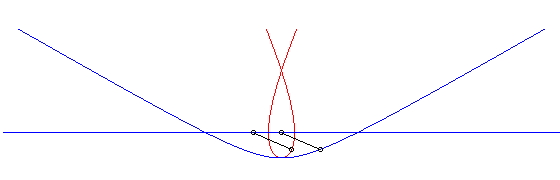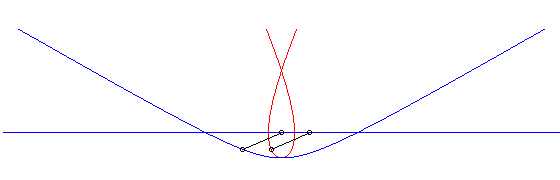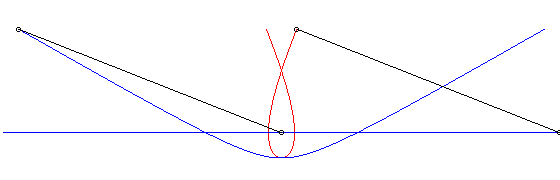
c) le crabe et l'initiateur ont, à un instant donné, des vitesses de sens contraire :

Paramétrisation cartésienne : , , .
Abscisse curviligne : .
Ci-contre, en bleu, est indiqué le mouvement hyperbolique du vecteur .

REMARQUE : Mannheim a montré que la courbe de Duporcq de paramètre e est la roulette à base rectiligne du pôle de la spirale de Sturm vérifiant .

II) Cas où l'initiateur décrit une courbe quelconque :

Équation différentielle vectorielle : 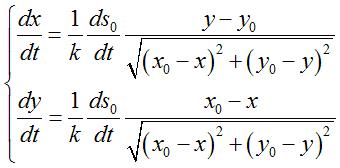, se traduisant par le système différentiel :
( = mobile initiateur, = crabe, ).

Pour un initiateur sur le cercle de centre O et de rayon R, on obtient le système différentiel : permettant de tracer les courbes à l'aide d'un logiciel.

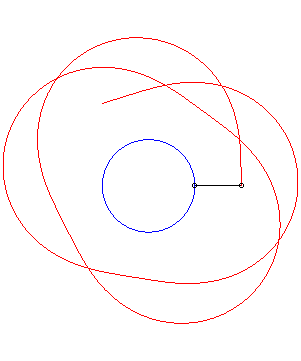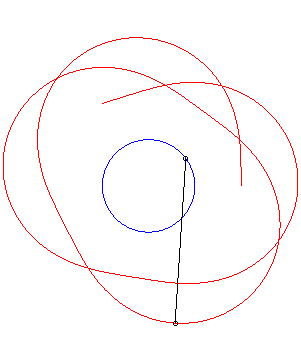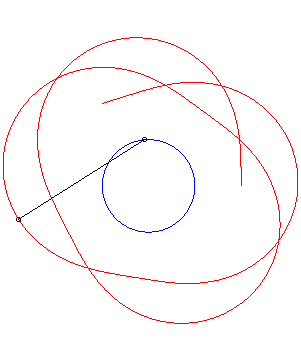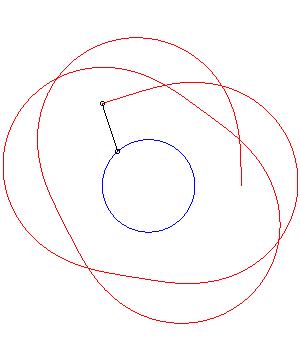
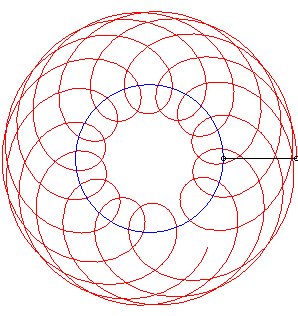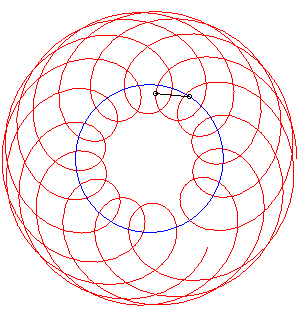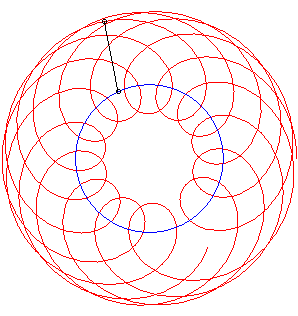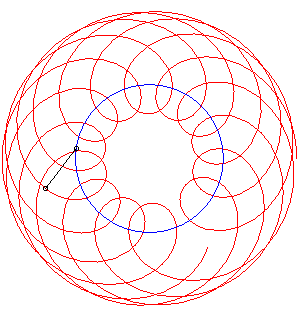
Un exemple avec k = 1.
Un exemple avec k = 1/3. La courbe de filature associée au mobile décrivant un cercle (en bleu ci-dessous) et à un point du cercle (l'arbre) fournit un cas particulier circulaire de courbe du crabe associée à un cercle.
Si est le rayon du cercle initiateur et R celui du cercle du crabe, on a .
Ci-dessous un exemple avec k = 1/2, .

VARIANTE (sur une idée d'Alain Esculier) : la vitesse du crabe n'est plus proportionnelle à celle de l'initiateur, mais à la distance à celui-ci.

Équation différentielle vectorielle : , se traduisant par le système différentiel linéaire : .
Équations du mouvement du crabe : .

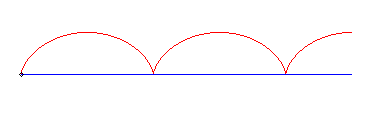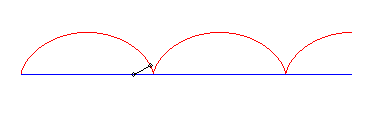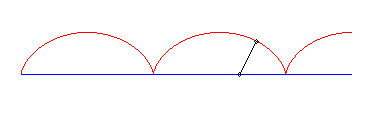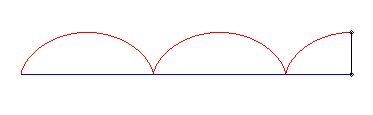
I) Initiateur rectiligne.

Pour un initiateur (vt, 0), équations du mouvement du crabe passant par (0, b) :
(a = v/k).
C'est donc une trochoïde de rapport , qui est une cycloïde si .

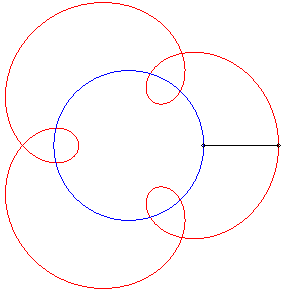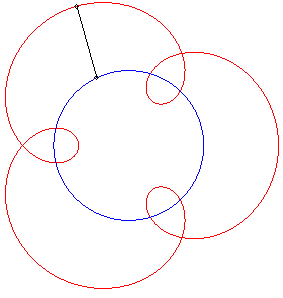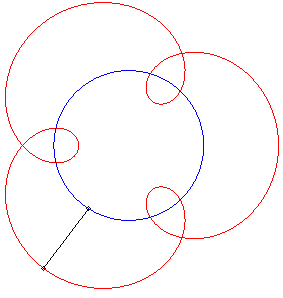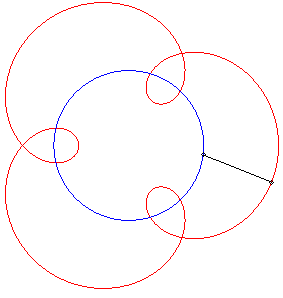
II) Initiateur circulaire.

Pour un initiateur, équations du mouvement du crabe passant par (0, a) pour :
. Il s'agit d'une épitrochoïde pour et d'une hypotrochoïde pour, épicycloïde et hypocycloïde pour a = R. Le paramètre q est égal à .

Pour , on obtient : , qui n'est autre qu'une développante de cercle (plus précisément, développante du cercle parcouru par l'initiateur).

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

Un exemple avec k = 1.	Un exemple avec k = 1/3.	La courbe de filature associée au mobile décrivant un cercle (en bleu ci-dessous) et à un point du cercle (l'arbre) fournit un cas particulier circulaire de courbe du crabe associée à un cercle. Si est le rayon du cercle initiateur et R celui du cercle du crabe, on a . Ci-dessous un exemple avec k = 1/2, .

Pour un initiateur, équations du mouvement du crabe passant par (0, a) pour : . Il s'agit d'une épitrochoïde pour et d'une hypotrochoïde pour, épicycloïde et hypocycloïde pour a = R. Le paramètre q est égal à .
Pour , on obtient : , qui n'est autre qu'une développante de cercle (plus précisément, développante du cercle parcouru par l'initiateur).