Spirale de Sturm

SPIRALE DE STURM
Sturm spiral, Sturmsche Spirale

Courbe étudiée par Sturm en 1857 et Masurel en 2014.
Autre nom, dans cet article : courbe de Mannheim.

Les spirales de Sturm sont les courbes telles que le rayon de courbure est en tout point proportionnel à la distance à un point fixe : .
Le cas particulier e = 1 est étudié à spirale de Norwich.

Équation différentielle : (p est le rayon podaire).
Intégrale première : , d'où l'équation polaire : .

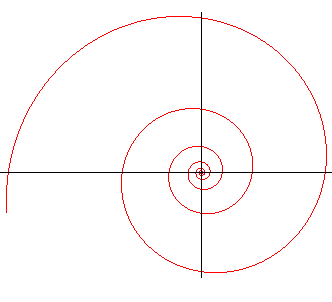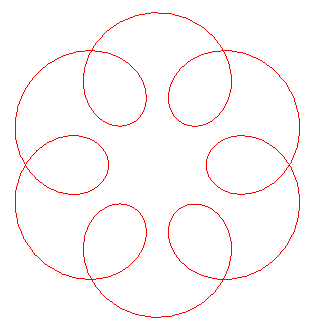
Si a = 0, alors , qui n'est autre qu'une spirale logarithmique, avec le cas limite du cercle pour e = 1 (pas de solution pour e < 1).

Cas elliptique, e<1
Paramétrisation cartésienne : 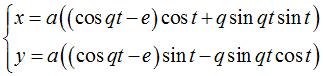où .
Paramétrisation complexe : (il s'agit donc d'une tritrochoïde).
Abscisse curviligne : . Angle tangentiel cartésien : .
Rayon de courbure :
Lorsque q est rationnel, l'ordre de la symétrie de rotation est égal au dénominateur de q moins 1.

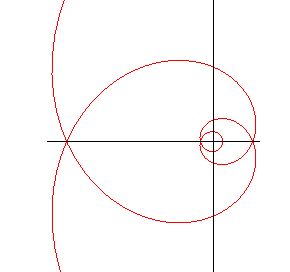
Cas hyperbolique, e >1
Paramétrisation cartésienne : où .
Abscisse curviligne : .
Angle tangentiel cartésien : .
Rayon de courbure : .

Propriétés remarquables (y compris dans le cas e = 1) :
     - La roulette à base rectiligne d'une spirale de Sturm est une courbe de Duporcq de même paramètre e (d'où l'utilisation de cette lettre e, associée à l'excentricité d'une conique).
    - la développée de la spirale de Sturm dans le cas elliptique est une épicycloïde
    - la développée de la spirale de Sturm dans le cas hyperbolique est une para- ou une hypercycloïde.

Considérons maintenant les courbes telles que la courbure est proportionnelle à la distance à un point fixe ; l'équation différentielle donne comme intégrale première , d'où l'équation polaire : ;

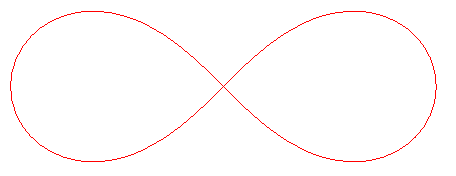
Le cas c = 0, donne qui n'est autre qu'une lemniscate de Bernoulli.
La courbure d'une lemniscate est proportionnelle à la distance au centre.

Enfin, l'une des solution de est la cardioïde.

Comparer avec la courbe élastique, ou radioïde aux abscisses, courbe telle que la courbure est proportionnelle à la distance à une droite fixe.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

Si a = 0, alors , qui n'est autre qu'une spirale logarithmique, avec le cas limite du cercle pour e = 1 (pas de solution pour e < 1).
Cas elliptique, e<1 Paramétrisation cartésienne : où . Paramétrisation complexe : (il s'agit donc d'une tritrochoïde). Abscisse curviligne : . Angle tangentiel cartésien : . Rayon de courbure : Lorsque q est rationnel, l'ordre de la symétrie de rotation est égal au dénominateur de q moins 1.
Cas hyperbolique, e >1 Paramétrisation cartésienne : où . Abscisse curviligne : . Angle tangentiel cartésien : . Rayon de courbure : .

Considérons maintenant les courbes telles que la courbure est proportionnelle à la distance à un point fixe ; l'équation différentielle donne comme intégrale première , d'où l'équation polaire : ;
Le cas c = 0, donne qui n'est autre qu'une lemniscate de Bernoulli.	La courbure d'une lemniscate est proportionnelle à la distance au centre.
Enfin, l'une des solution de est la cardioïde.