Trochoïde à centre

TROCHOÏDE À CENTRE, POLYTROCHOÏDE
Centred trochoid, zentrirte Trochoide

Courbe étudiée par Dürer (1525), Desargues (1640), Huygens (1679), Leibniz, Newton (1686), de L'Hôpital (1690), Jacob Bernoulli (1690), la Hire(1694), Johann Bernoulli (1695), Daniel Bernoulli (1725), Euler (1745, 1781).
Voir aussi : Eric Guiot, Trajectory under harmonic potential and magnetic force.

Paramétrisation complexe : , , et pour une épitrochoïde, pour une hypotrochoïde.
Équation différentielle : , soit .

Le terme de trochoïde à centre permet de regrouper les épi- et hypotrochoïdes. Les trochoïdes à centre sont donc les trajectoires des mouvements composé de deux mouvements circulaires uniformes.
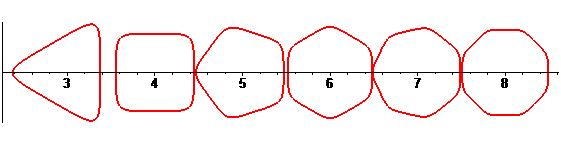
Elles contiennent les cycloïdes à centre (cas , vitesses égales) et les rosaces (cas , rayons égaux).
Lorsque (accélérations centripètes égales), on obtient les trochoïdes à méplat.

Epitrochoïdes à méplat (à commencer par le limaçon) Hypotrochoïdes à méplat

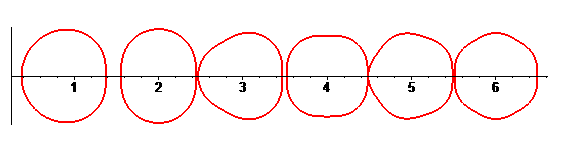Interprétation électromagnétique (voir lien Éric Guiot).
En écrivant l'équation différentielle sous la forme , on voit que ces courbes sont les trajectoires d'une particule chargée soumise à une force centrale d'intensité poportionnelle à la distance, et à un champ magnétique d'intensité constante perpendiculaire au plan de la courbe.
Avec , on a donc , et . On obtient alors une hypotrochoïde pour k < 0, et une épitrochoïde pour .
Notons que si , alors sont complexes conjugués, et on obtient alors une spirale de la tige en rotation.

L'expression peut être vue comme une somme vectorielle...

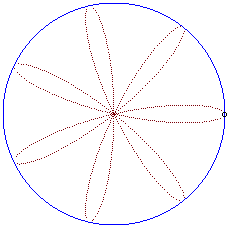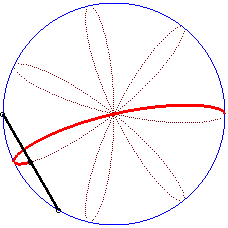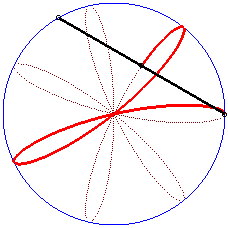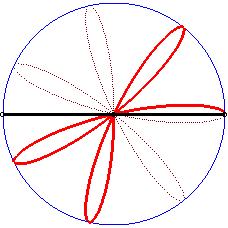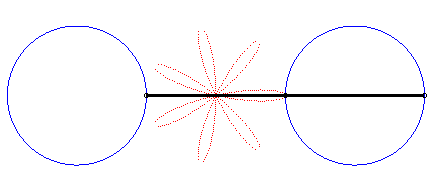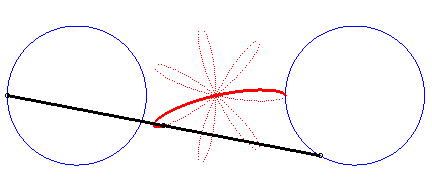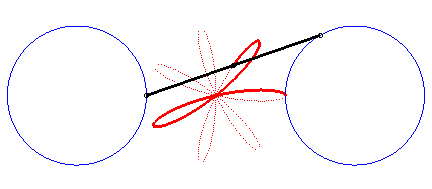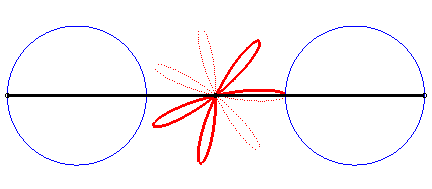
... ou comme milieu de deux points sous la forme ; les deux points décrivent des mouvements circulaires uniformes concentriques (ci-contre, un cas (rosace), les deux cercles sont identiques).

En écrivant 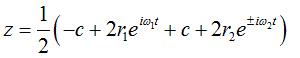, on peut séparer les cercles décrits par les deux points.

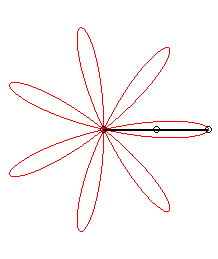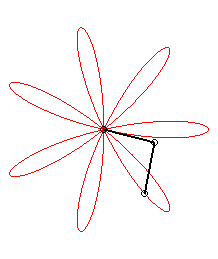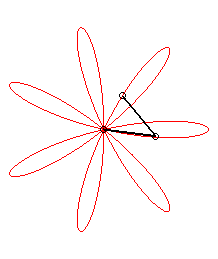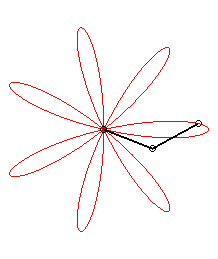
En écrivant , on obtient inversement toutes les trochoïdes à centres comme lieux des barycentres à coefficients donnés de deux mouvement circulaires uniformes sur le même cercle.

Et d'ailleurs tous les barycentres à coefficients fixés de deux points décrivant des mouvements circulaires uniformes décrivent des trochoïdes à centres.
Image réalisée avec geogebra par André Chauvière.

Les trochoïdes à centre sont aussi les projections sur le plan xOy des courbes des satellites.

Cette notion se généralise à la trajectoire d'un mouvement composé d'un nombre fini de n mouvements circulaires uniformes, de sens quelconques pouvant prendre le nom de polytrochoïde.

La trisectrice de Céva, la néphroïde de Freeth et la torpille sont des exemples de tritrochoïdes, ainsi que cet élégant quintifolium dissymétrique :
, .

C'est une trajectoire de ce type que parcourent ces adeptes des chaudrons magiques du parc Astérix ; les chaudrons décrivent des épitrochoïdes ; si le chaudron tourne sur lui même, la courbe décrite par les occupants est une tritrochoïde.

Autre exemple de tritrochoïde

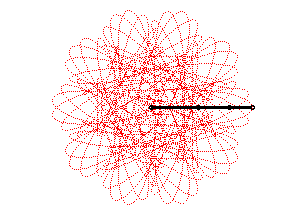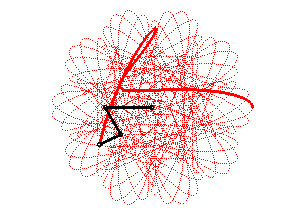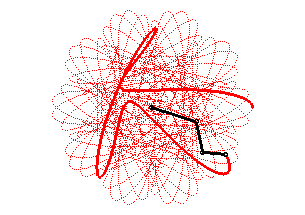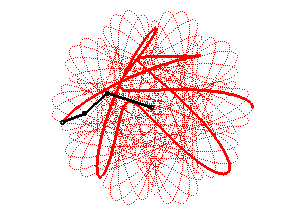Quitte à augmenter la valeur de n, on peut, par une polytrochoïde, approcher toute courbe ; voir par exemple cette page.

Un exemple de 2n +1-trochoïde est la 2n +1-sectrice de Céva de paramétrisation complexe .
Voir aussi les trochoïdes à base quelconque.
La généralisation à l'espace est la notion de trochoïde sphérique.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres


Epitrochoïdes à méplat (à commencer par le limaçon)	Hypotrochoïdes à méplat

L'expression peut être vue comme une somme vectorielle...
... ou comme milieu de deux points sous la forme ; les deux points décrivent des mouvements circulaires uniformes concentriques (ci-contre, un cas (rosace), les deux cercles sont identiques).
En écrivant , on peut séparer les cercles décrits par les deux points.
En écrivant , on obtient inversement toutes les trochoïdes à centres comme lieux des barycentres à coefficients donnés de deux mouvement circulaires uniformes sur le même cercle.
Et d'ailleurs tous les barycentres à coefficients fixés de deux points décrivant des mouvements circulaires uniformes décrivent des trochoïdes à centres. Image réalisée avec geogebra par André Chauvière.

La trisectrice de Céva, la néphroïde de Freeth et la torpille sont des exemples de tritrochoïdes, ainsi que cet élégant quintifolium dissymétrique : , .
C'est une trajectoire de ce type que parcourent ces adeptes des chaudrons magiques du parc Astérix ; les chaudrons décrivent des épitrochoïdes ; si le chaudron tourne sur lui même, la courbe décrite par les occupants est une tritrochoïde.
Autre exemple de tritrochoïde
Quitte à augmenter la valeur de n, on peut, par une polytrochoïde, approcher toute courbe ; voir par exemple cette page.