Paramétrisation cartésienne :  avec a=qb. provenant de  Courbe sphérique, algébrique ssi q = a/ b est rationnel (degré = 2(numérateur + dénominateur de q)).

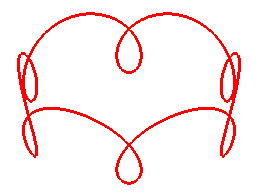
Une trochoïde sphérique est le lieu d'un point du plan mobile emmené par un cercle roulant sans glisser sur un cercle fixe, les deux cercles faisant un angle constant  ; ici, a est le rayon du cercle fixe, b celui du cercle mobile, d la distance du point au centre du cercle mobile et xOy le plan du cercle fixe.

Autrement dit : les trochoides sphériques sont les roulettes d'un mouvement sphère sur sphère dont la base et la roulante sont des cercles.

Pour d = b, on retrouve les cycloïdes sphériques, d'où les expressions parfois utilisées de cycloïde sphérique allongée (d > b) ou raccourcie (d < b) pour les trochoïdes sphériques.

Lorsque  = 0, on retrouve l’hypotrochoïde plane, et lorsque  = , l’épitrochoïde plane ; hormis ces deux cas, la trochoïde est tracée sur une sphère fixe, d’où son nom de trochoïde sphérique. Le centre W de cette sphère est le point de Oz de cote  et son rayon .

     .................

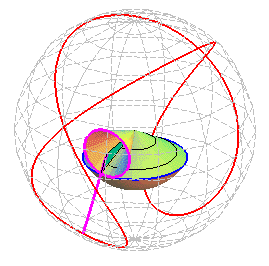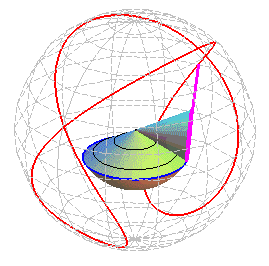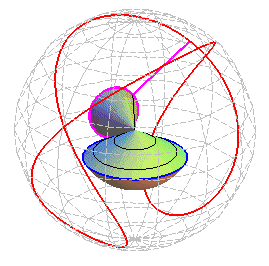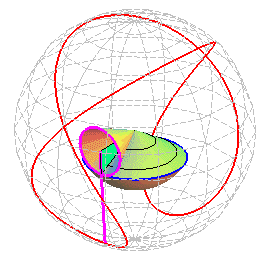
Lorsque le cercle roulant a même centre que la sphère, ce qui se traduit par d = R ou , on obtient les hélices sphériques.

On peut aussi voir la trochoïde comme la trajectoire de l'extrémité M d'un angle droit APM, où A est fixe, P a un mouvement circulaire uniforme autour d'un axe passant par A, et M a un mouvement circulaire uniforme autour de l'axe (AP). Ce faisant, on obtient toutes les trochoïdes sphériques, plus, lorsque P = A , les courbes des satellites.
 
 

Cette dernière définition n'est pas à confondre avec celle de la trajectoire de l'extrémité M d'un bras articulé APM, où A est fixe, P a un mouvement circulaire uniforme autour d'un axe passant par A, et M a un mouvement circulaire uniforme autour d'un axe passant par P (contrairement au cas plan où les notions de trochoïdes (à centre) et de double mouvement circulaire se confondent). Une telle trajectoire n'est pas sphérique. Par exemple, la trajectoire d'un point de la terre ou celle du centre de la lune par rapport au soleil est une telle courbe ; ce n'est pas une trochoïde sphérique, car l'axe de la terre reste parallèle à lui-même ; il n'est pas en rotation autour de l'axe de rotation de la terre autour du soleil.

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  Alain ESCULIER 2009