Cycloïde sphérique

CYCLOÏDE SPHÉRIQUE
Spherical cycloid, Kugelzykloide

Courbe étudiée par Jean Bernoulli en 1732, puis par Hachette en 1811, et par Reuleaux.

Paramétrisation cartésienne : .
Courbe sphérique, algébrique ssi q est rationnel (degré = 2(numérateur + dénominateur de q)).

Une cycloïde sphérique est le lieu d'un point d'un cercle roulant sans glisser sur un cercle fixe, les deux cercles faisant un angle constant ; ici, a est le rayon du cercle fixe, celui du cercle mobile et xOy le plan du cercle fixe.

Lorsque = 0, on retrouve l’hypocycloïde, et lorsque = , l’épicycloïde ; hormis ces deux cas, la cycloïde est tracée sur la sphère commune au cercle de roulement et au cercle roulant, d’où son nom de cycloïde sphérique. Le centre W de cette sphère est le point de Oz de cote et son rayon .
La cycloïde sphérique est donc une roulette d'un mouvement sphère sur sphère.

Sauf cas de dégénérescence, la cycloïde sphérique est donc aussi le lieu d'un point d'un cône de révolution roulant sans glisser sur un cône de révolution de même sommet : ces deux cônes sont les cônes de centre W contenant respectivement le cercle fixe et le cercle mobile.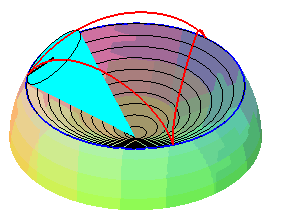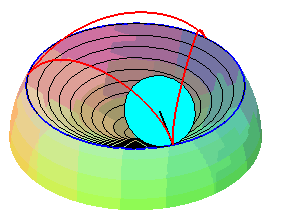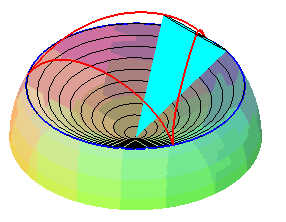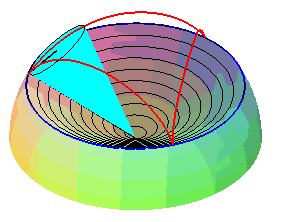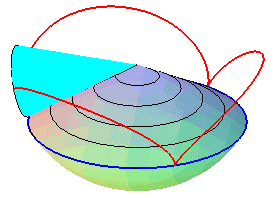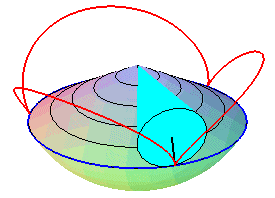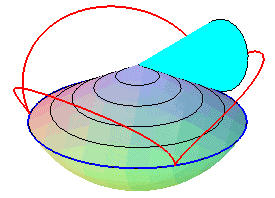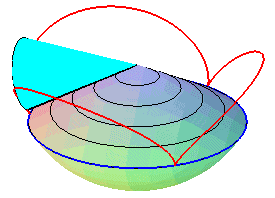

Les cycloïdes sphériques sont des courbes formées d'arcs isométriques (les arches) en nombre égal au numérateur du nombre q si q est rationnel et en nombre infini sinon.
Les arches se rejoignent en des points de rebroussements, obtenus pour situés sur le cercle de roulement, de cote 0, et ont des sommets situés sur le cercle de cote , de rayon .

Lorsque et , soit , le cercle des sommets est de rayon inférieur ou égal à celui du cercle de base, et l'on parle alors d'hypocycloïde sphérique.
Lorsque et , soit , ou lorsque , le cercle des sommets est de rayon supérieur ou égal à celui du cercle de base, et l'on parle alors d'épicycloïde sphérique.
Dans le cas intermédiaire , les cercle de base et des sommets ont même rayon, la courbe est une hélice sphérique ; dans ce cas, les sommets sont aussi des rebroussements, le cercle mobile est centré en W (c'est donc un grand cercle de la sphère) et roule sans glissser sur le cercle des sommets, et le cône roulant ci-dessus dégénère en un plan.
Si l'on change q en q/(q + 1) et en , les courbes ont même allure et les cercles des sommets ont même cote, mais ne sont pas égaux : contrairement au cas des épi- et hypocycloïdes planes, il n'y a pas de double génération.

cas : hypocycloïde

cas : épicycloïde cas : épicycloïde

cas : hélice sphérique.

cas , en rouge, et , en bleu.

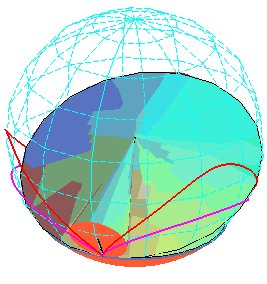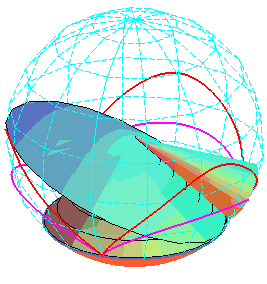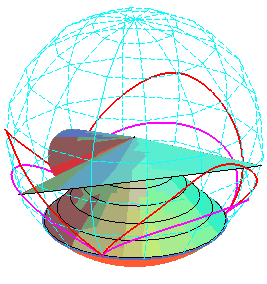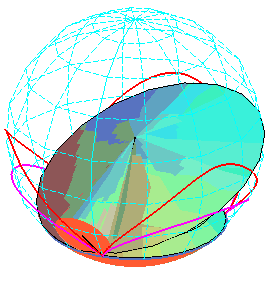Sur cette animation, les cercles des sommets des deux cycloïdes ont même rayon, mais pas même cote.

Cas particulier q = 1 (cercles de base et roulant de mêmes rayons) :

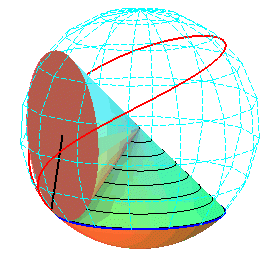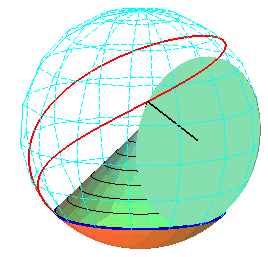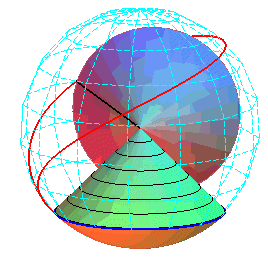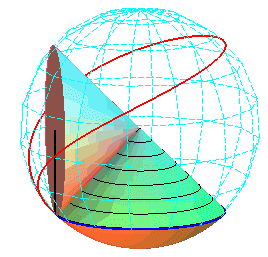
Paramétrisation cartésienne :

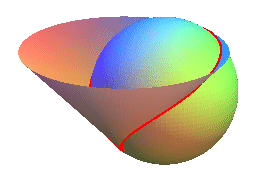
Les projections sur xOy, yOz, xOz sont respectivement une cardioïde, un arc de parabole et une goutte d'eau.

La courbe est l'intersection de la sphère avec le cône de révolution tangent en son sommet à la sphère ; c'est donc une biquadratique sphérique.

Les superbe modèles modèles ci-dessous montrent la génération des cycloïdes sphériques par roulement cône sur cône.

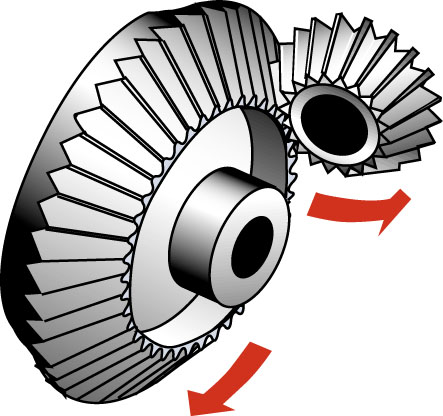Chaque point des roues de ces cyclistes décrit une épicycloïde sphérique. Les mouvements relatifs des engrenages coniques décrivent des épicycloïdes sphériques

Voir aussi les courbes de salkowski, et la généralisation aux trochoïdes sphériques.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres


Chaque point des roues de ces cyclistes décrit une épicycloïde sphérique.	Les mouvements relatifs des engrenages coniques décrivent des épicycloïdes sphériques