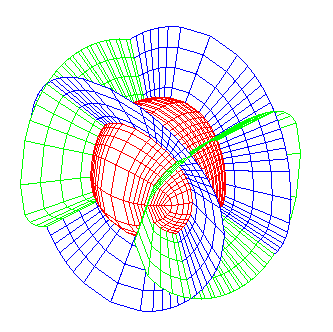
Famille de cônes elliptiques dessinant sur la sphère un système double orthogonal de biquadratiques ; voir à système triple orthogonal.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
BIQUADRATIQUE
Biquadratic
curve, biquadratische Kurve
| Autre nom : courbe quartique 3D de première espèce. |
Les biquadratiques sont les courbes algébriques
du quatrième degré intersections de deux quadriques
n'ayant pas une droite commune (auquel cas la courbe serait du troisième
degré).
On montre que les biquadratiques peuvent toutes être
obtenues comme intersections de deux cônes ou cylindres du second
degré (théorème dû à Poncelet). Lorsqu'il
s'agit de deux cylindres de révolution, la courbe est appelée
bicylindrique.
Si l'une des quadriques est une sphère, on parle de biquadratique sphérique, ou de cyclique sphérique, qui s'obtient toujours par intersection d'une sphère et d'un cylindre ou cône du second degré (théorème dû à Poncelet bis) ; exemples : les courbes sphéro-cylindriques (dont la courbe de Viviani), les ellipses sphériques, un cas particulier de cycloïde sphérique, et un autre exemple sur la page de la couture de la balle de tennis.
Autre exemple : la courbe de la crêpe, intersection d'un cylindre de révolution avec un cylindre parabolique.
Voir aussi les ovales de Descartes, les courbes de Both (dont la lemniscate de Bernoulli), la quartique de Külp, la conchoïde de Dürer, le bicorne, qui sont des projections planes de biquadratiques.

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2012