Un système triple orthogonal de surfaces consiste en la donnée de trois familles à un paramètre de surfaces telles qu'en chaque point commun à trois représentants de chaque famille, les trois plans tangents à chaque surface sont 2 à 2 orthogonaux. Cette notion généralise à la 3D la notion de système double orthogonal de courbes.
D'après le théorème de Dupin, deux surfaces, prises dans deux des familles du système, s'intersectent suivant des lignes de courbure.
 

Si les trois familles sont données sous forme paramétrique : , u fixé, v,w variables pour la première famille, v fixé, u,w variables pour la deuxième,  w fixé, u,v variables pour la troisième,  les trois familles forment un système triple orthogonal ssi  (autrement dit les colonnes de la jacobienne de  sont orthogonales 2 à 2).

Une première série d'exemples est fournie par la donnée d'un système double orthogonal  que l'on translate orthogonalement à son plan (les trois familles orthogonales sont formées de deux familles de cylindres construits sur les courbes de base et de la famille des plans orthogonaux à la direction de translation) ; le système triple orthogonal est alors paramétré par .
Quelques exemples (première famille, u fixé, en rouge, deuxième, v fixé, en bleu, troisième, w fixé, en vert) :
 
 

Système double orthogonal	système triple cylindrique associé	paramétrisation	équations des trois familles	nom du système de cordonnées (u,v,w)
	plans			coordonnées cartésiennes
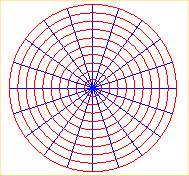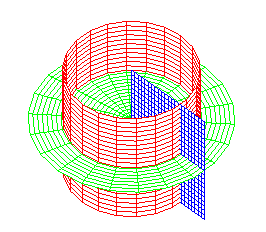
	cylindres de révolution, plans			coordonnées cylindriques
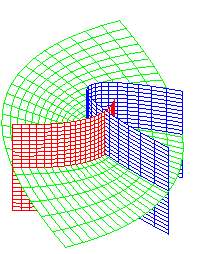
	cylindres paraboliques, plans			coordonnées cylindriques paraboliques
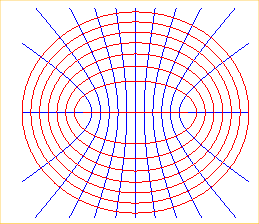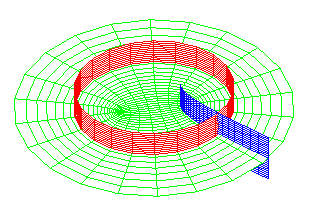
	cylindres elliptiques, cylindres hyperboliques, plans			coordonnées cylindriques elliptiques

Une deuxième série est fournie par la donnée d'un système double orthogonal  que l'on pivote autour d'un axe de son plan (plutôt un axe de symétrie pour éviter les points coniques) ; les trois familles orthogonales sont formées de deux familles de surfaces de révolutions construites sur les courbes de base et de la famille des plans passant par l'axe de rotation) ; si l'on pivote autour de Oz, le système triple orthogonal est alors paramétré par .
Quelques exemples :
 

Système double orthogonal	système triple de révolution associé	paramétrisation	équations des trois familles	nom du système de coordonnées (u,v,w)
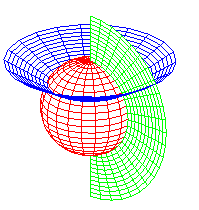
	sphères, cônes, plans			coordonnées sphériques
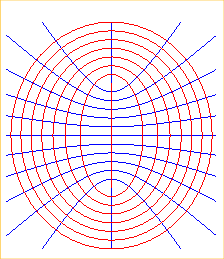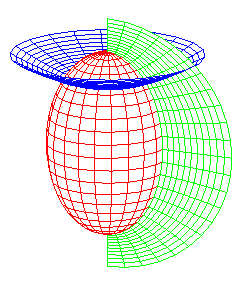
	ellipsoïdes allongés, hyperboloïdes à deux nappes, plans			coordonnées ellipsoïdiques allongées
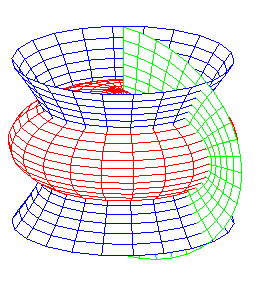
	ellipsoïdes aplatis, hyperboloïdes à une nappe, plans			coordonnées ellipsoïdiques aplaties
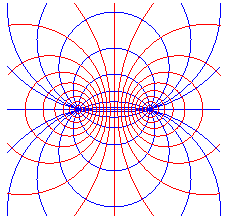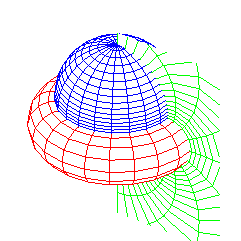
	tores à trou, sphères, plans			coordonnées toriques
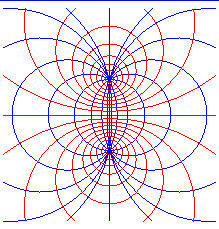	sphères, tores croisés, plans			coordonnées bisphériques

Une troisième série est obtenue par images par une inversion d'un système triple orthogonal, le système obtenu étant encore un système triple orthogonal (comme par toute transformation conforme).
 

Système orthogonal de départ	équivalent 2D	système triple	paramétrisation	équations des trois familles	nom du système de coordonnées (u,v,w)
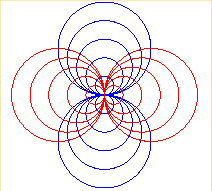plans orthogonaux (associés aux coordonnées cartésiennes)		= trois faisceaux singuliers de sphères orthogonaux			coordonnées trisphériques
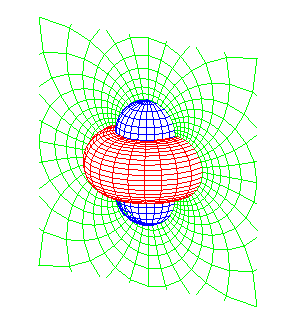
système associé aux coordonnées cylindriques	le système triple orthogonal inverse des coordonnées cylindriques n'est autre que ce système double formé de deux faisceaux de cercles orthogonaux tourné autour de Oz...	tores à trou nul, plans, sphères			coordonnées cylindriques inverses

Par inversion, les coordonnées sphériques redonnent elles-mêmes.

Quatrième série : systèmes de quadriques homofocales.
 

système triple	paramétrisation	intervalles de définition	équations des trois familles	Nom du système de coordonnées (u,v,w)
ellipsoïdes, hyperboloïdes à une nappe, hyperboloïdes à deux nappes		si  :		coordonnées ellipsoïdiques homofocales ; voir aussi à quadriques.
paraboloïdes elliptiques tournés vers le haut, paraboloïdes hyperboliques, paraboloïdes elliptiques tournés vers le bas		Si  :		coordonnées paraboloïdiques homofocales ; voir aussi à paraboloïde hyperbolique
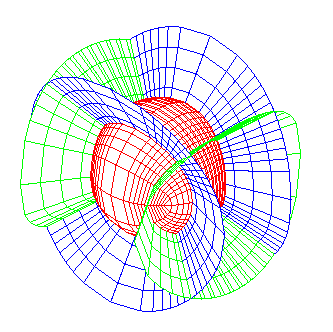sphères, cônes elliptiques. Remarquer le système double orthogonal de biquadratiques sur la sphère (rappelons que sur la sphère, toute ligne est de courbure).		Si  :		coordonnées coniques

 
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2012