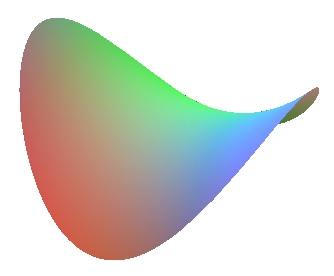
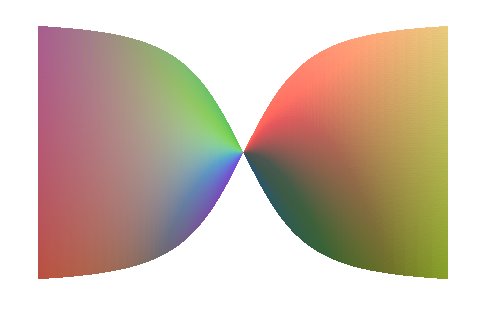
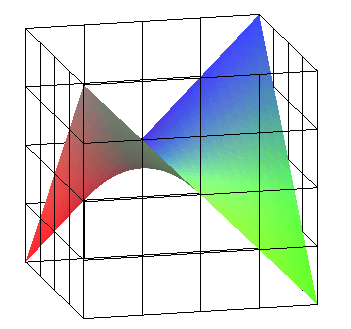
Paraboloïde hyperbolique

PARABOLOÏDE HYPERBOLIQUE
Hyperbolic paraboloid (HP-bowl), Hyperbolisches Paraboloid

Nom familiers : PH, voire péhache, ou selle de cheval

Équation cartésienne :

.
Quadrique doublement réglée.
Paramétrisations cartésiennes :

dont les lignes de coordonnées forment la double famille de droites (qui sont aussi les lignes asymptotiques) :
dont les lignes de coordonnées forment la double famille de paraboles génératrices en tant que surface de translation :
dont les lignes de coordonnées forment la famille des hyperboles horizontales et une famille de parabole :	ou
dont les lignes de coordonnées sont les lignes de courbure :		Les lignes de courbures se projettent sur xOy en un double réseau d'hyperboles dont l'un est donné par .

Lignes de striction : les 2 paraboles sections par les plans où (rectilignes et situées dans le plan z = 0 dans le cas équilatère) [Aubert et Papelier, t. III, p. 134]

Le paraboloïde est dit équilatère si a = b (les génératrices de chaque famille sont alors deux à deux orthogonales).
Équation cartésienne dans le cas équilatère :

(repère tourné de

autour de Oz,

).
Équation cylindrique :

.
Paramétrisations cartésiennes :

dont les lignes de coordonnées donnent la famille des hyperboles horizontales et une famille de paraboles :	ou
dont les lignes de coordonnées donnent une famille de droites et une famille d'horoptères :

Première forme quadratique fondamentale :

.
Élément d'aire :

.
Deuxième forme quadratique fondamentale :

.
Courbure de Gauss :

; tous les points sont hyperboliques.
Courbure moyenne :

Un paraboloïde hyperbolique peut être défini comme la surface réglée engendrée par les droites
- rencontrant deux droites non coplanaires en restant parallèles à un plan fixe (sécant à ces deux droites), appelé plan directeur du paraboloïde
- rencontrant trois droites 2 à 2 non coplanaires, mais parallèles à un plan donné (lorsque ce n'est pas le cas, on obtient l'hyperboloïde à une nappe).

On peut aussi définir un paraboloïde hyperbolique comme la réunion des droites joignant deux points se déplaçant à vitesse constante sur deux droites non coplanaires.
Un quadrilatère gauche quelconque a donc ses 4 côtés inclus dans un unique PH (voir ce lien pour des précisions) ; malheureusement ce PH n'est pas en général la surface d'aire minimale s'appuyant sur ce contour (voir un cas particulier à surface de Schwarz).
Voir aussi le berlingot.

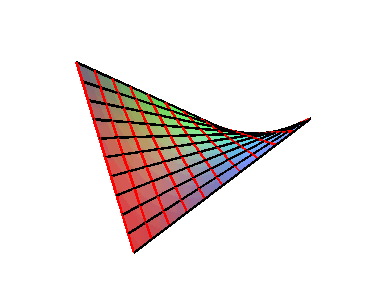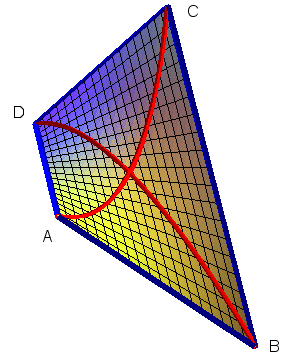
Si le quadrilatère gauche est ABCD, le PH correspondant est paramétré par , de sorte que , , , .
En rouge les deux paraboles diagonales u = v et u = 1–v dont le point d'intersection est l'isobarycentre du tétraèdre ABCD.
Voir aussi le patch de Coons qui généralise cette construction au cas où les côtés sont courbes.

On réalise donc une portion de paraboloïde hyperbolique en tendant des élastiques entre deux tiges rectilignes (les élastiques étant accrochés de façon régulière sur les tiges).

Dans les équations ci-dessus, le paraboloïde est la réunion des droites parallèles au plan directeur (qui est aussi asymptote) (P) : et également la réunion des droites parallèles au plan directeur (P') : .
Le paraboloïde hyperbolique est doublement un conoïde ; plus précisément, c'est un conoïde d'axe l'une des droites , de plan directeur (P') et de directrice une autre droite , et un conoïde d'axe l'une des droites , de plan directeur (P) et de directrice une autre droite .
Le cas équilatère (a = b) correspond au cas du conoïde droit, et c'est un cas particulier de conoïde de Zindler généralisé.

C’est également une surface de translation (translation d’une parabole le long d’une autre, orientée en sens inverse).

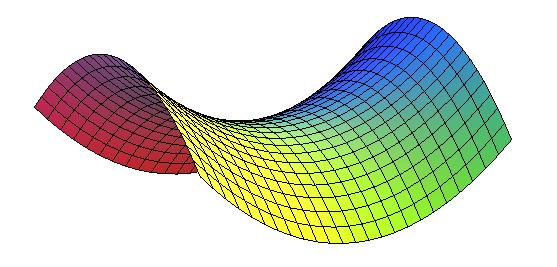
Les sections par des plans parallèles à Oz sont des paraboles, et les autres sections planes sont des hyperboles éventuellemnt dégénérées.

Dans le cas équilatère, les sections par des cylindres d'axe Oz sont des courbes de la crêpe.

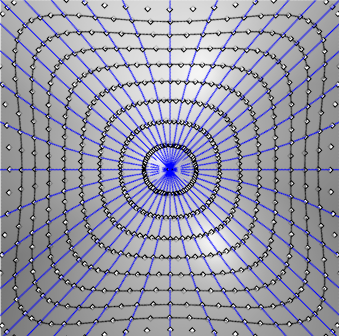
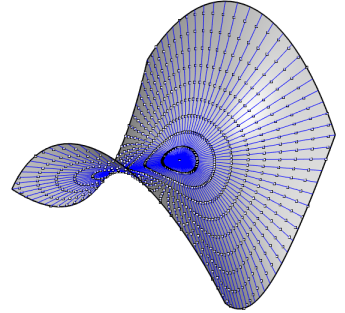
Les projections sur xOy des géodésiques du PH équilatère z = xy sont les courbes solutions de l'équation différentielle : .
Sont tracées sur cette figure les géodésiques issues de O et les "cercles géodésiques" correspondants.

Paraboloïdes confocaux et famille triple orthogonale de paraboloïdes.
Si a > b, les paraboloïdes d'équation sont tels que les sections par le plan xOz sont des paraboles confocales (i.e. de même foyer ).
Pour on obtient une première famille, formée de paraboloïdes elliptiques, pour on obtient une deuxième famille, formée de paraboloïdes hyperboliques, pour , une troisième famille, formée de nouveau de paraboloïdes elliptiques.
De plus ces trois familles forment une famille triple orthogonale, ce qui signifie chaque surface de chaque famille coupe orthogonalement chaque surface des deux autres familles (généralisation 3D des trajectoires orthogonales 2D).
Les lignes d'intersection sont des lignes de courbure (théorème de Dupin).
Ci-contre, un exemple de chaque famille.

Voir aussi les surfaces retournables, les surfaces de Bézier et la selle pour singe.

Jeu pour enfants, boulevard Richard Lenoir à Paris.
Les cordes suivent (plus ou moins) les droites du PH ...
Ici, Place Bellecour à Lyon.
On peut considérer que les cordes suivent les géodésiques et les cercles géodésiques..

Structure formée de 12 portions de paraboloïdes hyperboliques ; les 8 génératrices obliques (joignant 2 milieux de côté de carrés) sont des génératrices d'un hyperboloïde de révolution.
Si l'on remplace les paraboloïdes hyperbolique par la surface minimale s'appuyant sur les bords, on obtient le motif de base de la surface minimale P de Schwarz.

Sculpture d'Angel DUARTE en morceaux de paraboloïdes hyperboliques (Lausanne, Suisse) utilisant cette structure. Elle possède 36 portions de paraboloïdes hyperboliques.
Explication de cette structure.
Comparer avec la surface minimale P de Schwarz.

Restaurant Los Manantiales à Mexico
Architecte : F. Candela 1958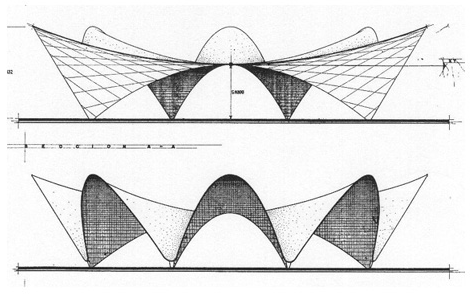

Voûtes à l'intérieur de la Sagrada Familia à Barcelone.
Architecte : Antoni Gaudi, qui a beaucoup utilisé les PH.

Église de Becerril de la Sierra (Espagne)
Architecte : Fr. Francisco Coello de Portugal
Le Palais du Cnit à Paris, dont la forme rappelle celle du paraboloïde hyperbolique,
est en fait, en première approximation, la réunion de trois cylindres paraboliques.

Voir d'autres belles photos sur la page du mathouriste.

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres

On peut aussi définir un paraboloïde hyperbolique comme la réunion des droites joignant deux points se déplaçant à vitesse constante sur deux droites non coplanaires. Un quadrilatère gauche quelconque a donc ses 4 côtés inclus dans un unique PH (voir ce lien pour des précisions) ; malheureusement ce PH n'est pas en général la surface d'aire minimale s'appuyant sur ce contour (voir un cas particulier à surface de Schwarz). Voir aussi le berlingot.
Si le quadrilatère gauche est ABCD, le PH correspondant est paramétré par , de sorte que , , , . En rouge les deux paraboles diagonales u = v et u = 1–v dont le point d'intersection est l'isobarycentre du tétraèdre ABCD. Voir aussi le patch de Coons qui généralise cette construction au cas où les côtés sont courbes.
On réalise donc une portion de paraboloïde hyperbolique en tendant des élastiques entre deux tiges rectilignes (les élastiques étant accrochés de façon régulière sur les tiges).