CONOÏDE DE ZINDLER
Zindler's
conoid, Zindlersches Konoid
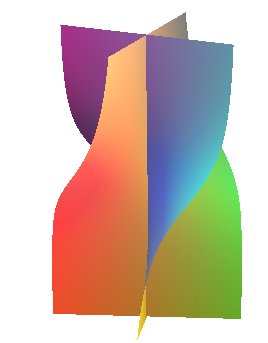
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CONOÏDE DE ZINDLER
Zindler's
conoid, Zindlersches Konoid
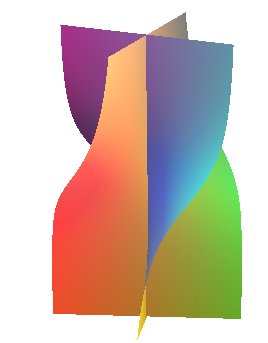
| Konrad Zindler (1866 -1934) : mathématicien autrichien. |
| Équation cylindrique : Paramétrisation cartésienne : Équation cartésienne : Surface cubique réglée, rationnelle de ligne double Oz. |
Le conoïde de Zindler est le conoïde
droit de directrice une couronne
tangentoïdale à 4 branches (ici, la couronne
) et d'axe l'axe de cette couronne.
Le conoïde de Zindler est aussi le conoïde
droit de directrice une cubique du type  située dans un plan parallèle à son axe.
située dans un plan parallèle à son axe.
Tout cylindre de génératrice Oz et de directrice une hyperbole équilatère perpendiculaire à l'axe coupe le conoïde de Zindler en une hyperbole (en rouge) plus l'axe Oz (en bleu).
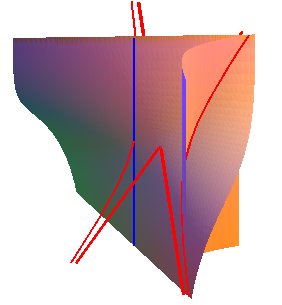
L'affinité complexe
le transforme en un conoïde de
Plücker, mais ces deux conoïdes ne sont pas images l'un de
l'autre par homographie réelle.
On peut généraliser à une couronne
tangentoïdale quelconque, ce qui donne l'équation cylindrique
: ;
| Le cas n = 1 donne alors le paraboloïde
hyperbolique équilatère |
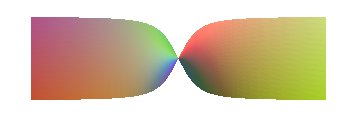 |

Cas n = 3
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL L.G. VIDIANI 2013