n = 1
n = 2
n = 3
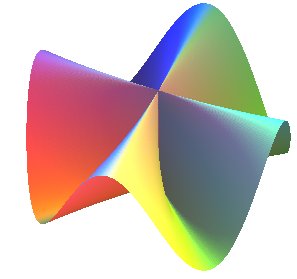
n = 4
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CONOÏDE DE PLÜCKER
Plücker's
conoid, Plückersches Konoid
|
n = 1 |
n = 2 |
|
n = 3 |
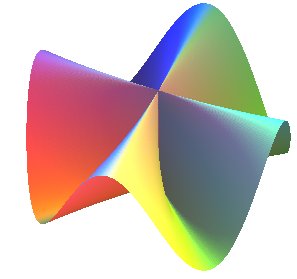
n = 4 |
| Julius Plücker (1801-1868) : mathématicien
et physicien allemand.
Autre nom : cylindroïde (de Plücker). Voir la programmation povray sur le site d'Alain Esculier. Voir le pb de centrale 94. |
Équation cylindrique : 
(surface à symétrie
de rotation).
Paramétrisation cartésienne :  ( ).
Équation cartésienne pour n entier :  .
Surface algébrique rationnelle si n = p/q est rationnel, de degré p + q pour p pair, 2(p + q) pour p impair. Première forme quadratique fondamentale :  .
Deuxième forme quadratique fondamentale :  .
Lignes asymptotiques : les génératrices et les courbes se projetant sur xOy en les spirales sinusoïdales :  . |
Un conoïde de Plücker général
peut être défini comme un conoïde
droit de directrice une couronne
sinusoïdale (ici, la couronne 
) et d'axe l'axe de cette couronne.
Le cas habituel est le cas n = 2 (la directrice est une courbe de la crêpe), qui est appelé en général conoïde de Plücker tout court :
Équation cartésienne :  .
Surface cubique réglée, rationnelle. (Rem : la surface algébrique complète, d'équation  ,
comprend aussi l'axe Oz entier)
Équation cylindrique :  .
Paramétrisation cartésienne :  ().
En tournant d'un huitième de tour, on obtient successivement les équations :  ,  ,
et  .
Première forme quadratique fondamentale :  ,
avec  .
Deuxième forme quadratique fondamentale :  ,
avec  .
|
| Le conoïde de Plücker possède deux plans de symétrie ; la section par un plan parallèle à un plan de symétrie est une cubique d'Agnesi et par un plan parallèle à un plan bissecteur des plans de symétrie, une anguinée. | ||
|
Voir aussi ici son invariance par retournement.
Il se traverse lui-même suivant le segment de Oz formé des points d'ordonnée entre -a et a, avec deux points pince aux extrémités.
On en obtient facilement une représentation matérielle en évidant un carré dans une feuille de papier et en joignant bord à bord les 4 côtés de ce carré (construction due à David Hanau, élève de PCSI).
Cette surface est susceptible de nombreuses définitions
géométriques provenant de la propriété suivante
:
Le cylindre de révolution de génératrice
Oz
:
coupe le
conoïde de Plücker en une ellipse dont le plan a pour équation
: 
, plus
l'axe Oz.
Le conoïde de Plücker est donc aussi la surface engendrée par les perpendiculaires communes à une droite fixe (D) = (Oz) et aux droites d'un plan fixe (P) non perpendiculaire à (D) passant par un point fixe de (P).
C'est le seul conoïde tel que quel que soit le point M, le lieu du projeté de M sur les génératrices du conoïde soit une courbe plane (qui est alors une ellipse).
Son inverse par rapport à un point de l’axe hors du segment d’auto-intersection est un bonnet croisé, ce qui en fait donc une représentation du plan projectif.
Il est également projectivement équivalent au parapluie de Whitney et au conoïde de Zindler, mais avec une homographie complexe seulement pour ce dernier.
Lien
vers une figure manipulable à la souris et montrant un ruban
de Möbius tracé sur ce conoïde.
 |
Construction réalisée par les élèves
de l'école d'architecture de Lyon.
Il s'agit d'une portion de conoïde droit de directrice un cercle passant par l'axe et faisant un angle de 45° avec lui, donc image par une dilatation d'un conoïde de Plücker. Photo dûe à Robert March
|
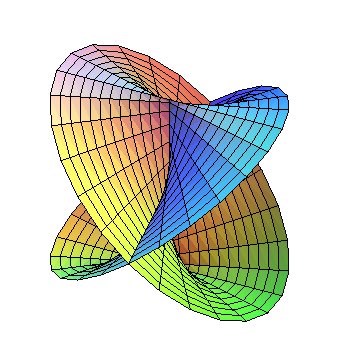
Cas n = 1 :
|
Paramétrisation cartésienne : 
(, une directrice
est l’ellipse centrée en O  ).
Équation cartésienne :  .
Surface quartique réglée rationnelle. Équation cylindrique :  . |
 |
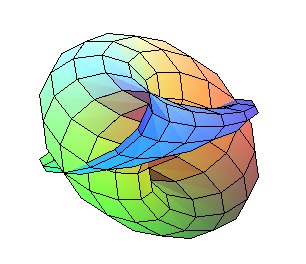
La section par le cylindre plein 
est aussi paramétrée par  .
Équation cartésienne dans ce cas :  . |
 |
Ce conoïde est une réunion d’ellipses dont
les sommets se trouvent sur les droites y = 0 et 
.
C'est aussi le lieu des tangentes à la sphère
de centre (a, 0, 0) et de rayon a, parallèles au plan
xOy,
et rencontrant l’axe Oz. Le lieu des points de tangence avec la
sphère est alors la fenêtre
de Viviani :  .
Voir le cas général sur la page du conoïde. |
Une ellipse en bleu, et la fenêtre de Viviani en rouge. |
La section de ce conoïde
avec le cône de révolution 
donne une courbe gauche se projetant sur xOy en le limaçon
de Pascal.
; ci-contre, le cas b = a, donnant la cardioïde. |
 |
Les sections des conoïdes de Plücker généralisés  avec
la sphère de centre O et de rayon a sont les clélies.
Plus généralement, les sections avec le tore de centre O et de rayon mineur a sont les solénoïdes toriques. Ci-contre, deux cas où n = 3. |
 |
 |
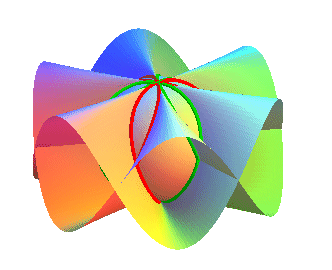Comparer les conoïdes de Plücker avec les cônes
sinusoïdaux.
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2018
,
ainsi que les génératrices.
