
une couleur = un tour autour de l'axe
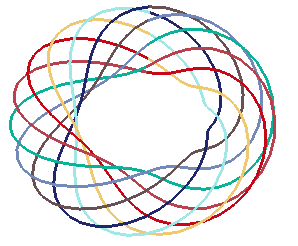
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SOLÉNOÏDE, NOEUD ET ENTRELACS TORIQUE
Torus
solenoid, knot and link, Torussolenoid, Torusknoten

une couleur = un tour autour de l'axe |
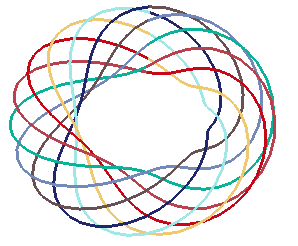 |
| Sites :
Wikipedia Knot atlas |
| Équation cylindrique : Paramétrisation cartésienne : Abscisse curviligne : |
Les solénoïdes toriques sont les solénoïdes
dont la courbe centrale est un cercle ; ils s'enroulent donc régulièrement
autour d'un tore. On peut
aussi les voir comme trajectoire d'un point ayant un mouvement circulaire
uniforme dans un plan tournant uniformément autour d'un axe.
| Les solénoïdes toriques sont aussi obtenus
par l'intersection du conoïde
de Plücker généralisé : |
 |
 |
Lorsque le tore est réduit à une sphère
(R = 0), on retrouve les clélies.
Les projections sur xOy sont les conchoïdes
de rosaces.
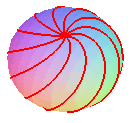
tore croisé |
 |

Vue de dessus : conchoïde de rosace. |
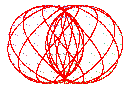 |

tore ouvert |
 |

Vue de dessus : conchoïde de rosace. |
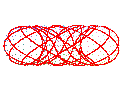 |
Lorsque n est un rationnel p/q, et R > r, la courbe est fermée et simple, et le noeud associé au solénoïde torique correspondant est le noeud torique T(p, q), possédant p enroulements autour du tore pour q tours autour de l'axe, qui est toujours un noeud premier. Les noeuds T(p, q) et T(q, p), sont équivalents (pour passer du (p, q) au (q, p), passer une aiguille dans l'âme du tore).
Tout noeud ayant une représentation sans croisement
sur le tore est un noeud torique de ce type.
Chaque section droite du tube comporte q brins
et la vue de dessus comporte p (q – 1) croisements ; il a
été démontré que pour p > q,
ce nombre de croisements est le nombre de croisements minimal du noeud
correspondant, (ce dernier nombre vaut donc q (p – 1)
pour
p < q).
| Pour n = 1 (et aussi pour n entier ou inverse d'entier), on obtient le noeud trivial (mais contrairement à ce qu'on pourrait attendre, le solénoïde n'est pas un cercle de Villarceau du tore). |  |
Pour q = 2 (resp. p = 2), on obtient
des noeuds à
p (resp. q) croisements :
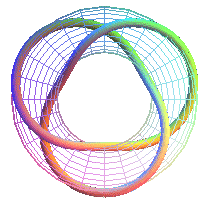
T(3,2) : noeud de trèfle noeud premier 31 |
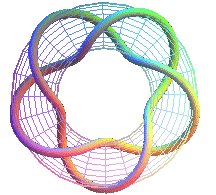
T(5,2) : pentagrame noeud premier 51 |
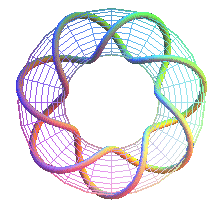
T(7,2) : premier heptagramme noeud premier 71 |
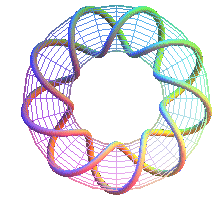
T(9,2) : premier nonagramme noeud premier 91 |
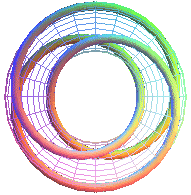 |
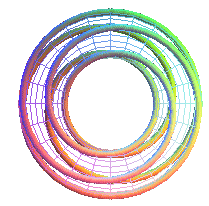
T(2,5) |
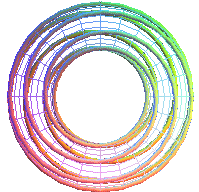
T(2,7) |

T(2,9) |
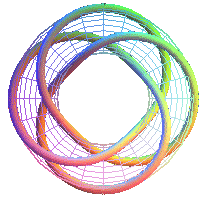
T(4,3) équivalent au 19ème noeud premier à 8 croisements |
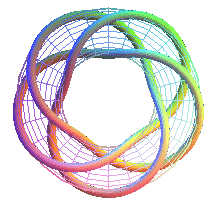
T(5,3) équivalent au 124ème noeud premier à 10 croisements |
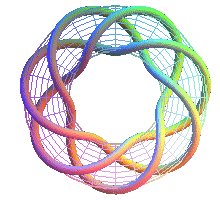
T(7,3) deuxième heptagramme |
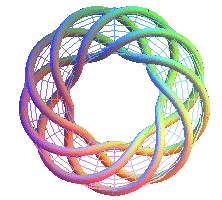
T(9,4) troisième nonagramme |
Les solénoïdes torique pour q = 2 sont
des bords de rubans de Möbius
à p torsions :

n = 1/2 : bord du ruban de Möbius classique (une torsion) |
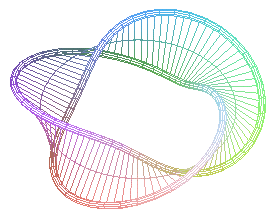
n = 3/2 : bord du ruban de Möbius à 3 torsions. |
| Lorsque p et q ne sont pas premiers entre
eux, si l'on pose d = pgcd(p, q), p' = p/d, q'
= q/d, n = p/q = p'/q', le solénoïde torique de type (p',
q') et ses d – 1 images par les rotations successives d'angle |
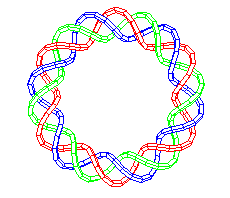 |
Voici quelques exemples :
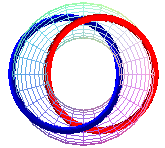
T (2,2), entrelacs de Hopf, entrelacs premier 212 |
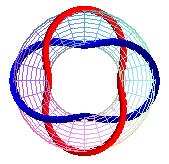
T(4,2), noeud de Salomon, entrelacs premier 412 |

T(3,3), entrelacs premier
633
|

T(6,2), entrelacs premier 612 |

T(6,3) |

T(6,4), deux noeuds de trèfle enlacés |

T(8,2) entrelacs premier 812 |
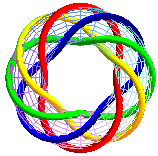
T(8,4) |

T(8,6) |

T(9,3) |
On peut réaliser l'entrelacs torique T(p,
q)
en prenant q brins de même longueur mis côte à
côte, en effectuant une torsion de p q-ièmes
de tours et en recollant les brins bout à bout.
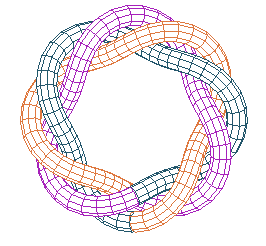
Par exemple pour le noeud (8, 3), il y a trois brins recollés après une torsion de 8 tiers de tours |

Ce même noeud en scultpture par J. Robinson Philip Trust Collection |
Les noeuds toriques sont aussi parfois définis
sur le tore de Clifford
; leur paramétrisation y est beaucoup plus simple :
; par identification de
avec
,
on peut les voir aussi comme l'image du cercle unité
par l'application :
.
Les noeuds et entrelacs toriques pour p > 2q
sont équivalents aux noeuds
et entrelacs polygrammiques.
Ce sont aussi les "arêtes" des prismes
rotoïdaux.
Le noeud torique de T(n, n–1) est équivalent
au noeud de trèfle à
n
feuilles.
Comparer avec les bonnets
turcs, qui ont la même vue de dessus, mais des croisements alternés.
Comparer aussi avec les géodésiques
du tore.
 |

Logo ChatGPT |

Gravure d'Escher |

Logo entreprise mexicaine |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2024