QUARTIQUE DE KÜLP
Kulp quartic,
Külpsche Quartik
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
QUARTIQUE DE KÜLP
Kulp quartic,
Külpsche Quartik
| Courbe étudiée par Külp en 1868 (archiv
der Math. und Physik p. 97) et Goormaghtigh
en 1913.
Ludwig Külp (1835 - 1891) : physicien allemand. Autre nom : conchoïde de Külp (à cause de la ressemblance avec la conchoïde de droite). |
 |
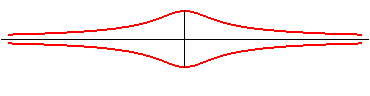Paramétrisation cartésienne :  .
Équation cartésienne : 
soit  .
Quartique rationnelle. |
La quartique de Külp est l'hyperbolisme du cercle par rapport à son centre et une tangente (cas particulier d'oeuf de Granville).
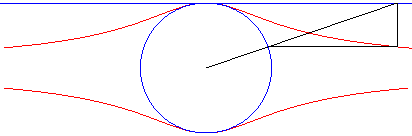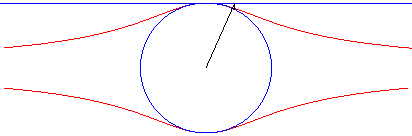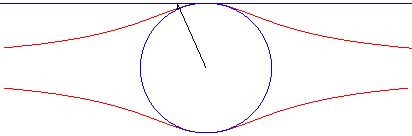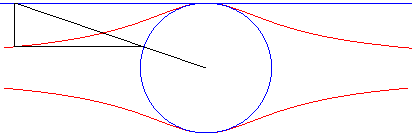
Ici, le cercle est le cercle de diamètre [OA] avec A(0, a) et la droite, y = a.
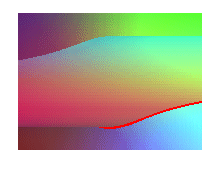
La quartique de Külp est aussi la projection sur
le plan xOy de la biquadratique
intersection du cylindre
de révolution : 
et du paraboloïde
hyperbolique : 
.
et d'équation cartésienne : 
qui lui est très proche :
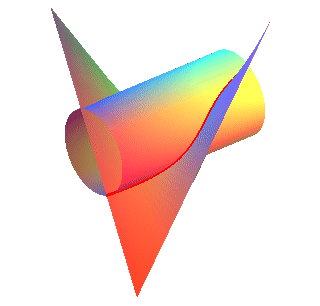
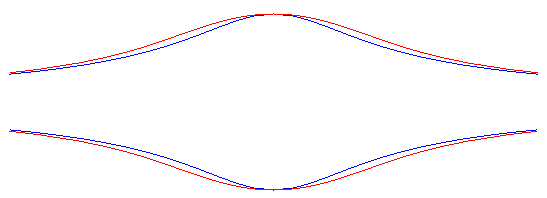
Comparer aussi avec la cubique
d'Agnesi.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2019