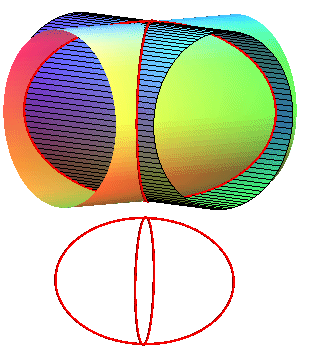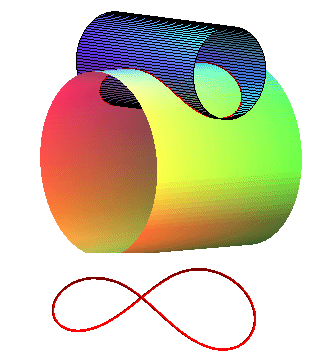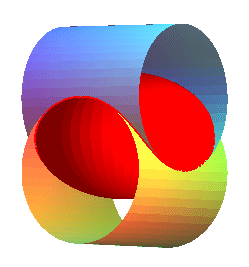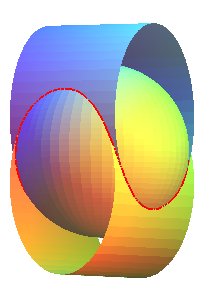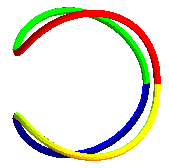Bicylindrique

BICYLINDRIQUE
Bicylindrical curve, dizylindrische Kurve

Les bicylindriques sont les courbes intersections de deux cylindres de révolution.

Première étude : cas de 2 cylindres orthogonaux, de rayons a et b, et d'axes distants de 2c :

Système d’équations cartésiennes :.
Biquadratique.
Paramétrisation cartésienne : .
Equation cartésienne de la projection sur xOy : (voir la courbe d'Alain).
Pour et c = 0 :
- Aire de la portion de cylindre délimitée par chaque composante, donnée par une intégrale elliptique de deuxième espèce : , se réduisant à 4a² pour a = b.
- Volume de la portion du grand cylindre découpée par le petit, donnée par des intégrales elliptiques de première et deuxième espèce :
, se réduisant à 16a³/3 pour a = b.

Cas a = b :
La courbe est invariante par les 2 retournements qui échangent les deux cylindres.

c = 0 : c'est la réunion de deux ellipses d'excentricité se coupant en leurs sommets secondaires à angle droit.

c petit.

c = a /2

Cas a < b ;

(ici c = 0) : courbe à deux composantes.
: courbe en huit courbé similaire à l'hippopède.
Voir la courbe d'Alain. : courbe à une composante.

On peut remarquer que cette bicylindrique est tracée sur l'ellipsoïde .
Par dilatation, on peut ramener l'ellipsoïde à une sphère, les deux cylindres devenant, eux, elliptiques. L'intersection obtenue est une des possibilités de la couture de balle de tenis.

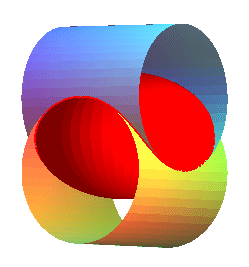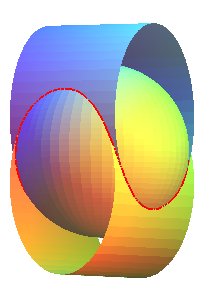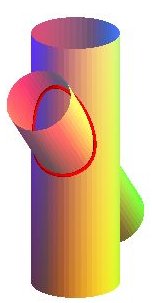
Les enroulements des courbes d'isoénergie du pendule pesant sont les bicylindriques intersections de cylindres d'axes perpendiculaires.

Deuxième étude : cas de deux cylindres d'axes sécants, l'un de rayon a, l'autre de rayon b, faisant un angle 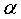avec le plan orthogonal au premier.

Système d’équations cartésiennes : .
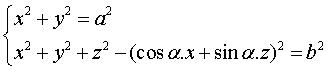Paramétrisation cartésienne : 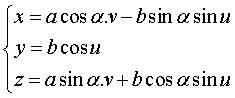, où .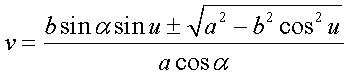
Cas a = b : 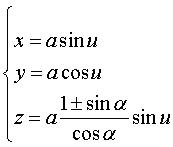, réunion de deux ellipses. 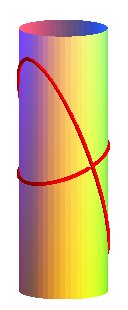Cas a = b

Le Joaillier suisse Philippe Mingard utilise des bicylindriques dans ses créations (cas a = b, c petit) ; il trouve que cette courbe est "la manifestation de la simplicité et de la pureté incarnées".
Voir aussi dans ce cas la couture de la balle de tennis, ou la courbe de la crêpe, autres courbes invariantes par retournement.

Le rulpidon d'Ulysse Lacoste, solide de Steinmetz percé de deux cylindres pleins, fait apparaître 10 arêtes qui sont 5 bicylindriques dont l'une est formée de deux ellipses.

Tombeau de Chateaubriant

Les poutres de mon chalet...
Station Botzaris, dans le métro parisien.
Les luminaires de mon escalier

De nombreux autres exemples sur la page du mathouriste !

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

Le Joaillier suisse Philippe Mingard utilise des bicylindriques dans ses créations (cas a = b, c petit) ; il trouve que cette courbe est "la manifestation de la simplicité et de la pureté incarnées". Voir aussi dans ce cas la couture de la balle de tennis, ou la courbe de la crêpe, autres courbes invariantes par retournement.
Le rulpidon d'Ulysse Lacoste, solide de Steinmetz percé de deux cylindres pleins, fait apparaître 10 arêtes qui sont 5 bicylindriques dont l'une est formée de deux ellipses.