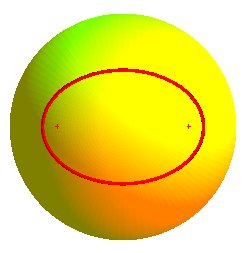
Ellipse sphérique

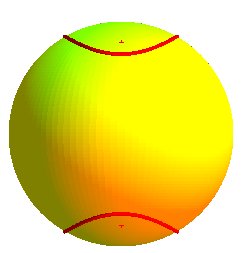
Hyperbole sphérique

 

Courbe étudiée par Fuss en 1788, Steiner en 1827, Chasles en 1831. Autre nom : conique sphérique. Site : www.geometrie.tuwien.ac.at/theses/pdf/diplomarbeit_tranacher.pdf

 

Coordonnées sphériques des foyers F, F': (la 3ème coordonnée étant la colatitude), soit . Équation bifocale de l'ellipse sphérique sur la sphère de rayon R :  (distance géodésique). Équation bifocale de l'hyperbole sphérique :  où G est le symétrique de F par rapport à xOy. Équation cartésienne de la courbe complète : section de la sphère  avec  le cône elliptique avec ,  le cylindre elliptique parallèle à Oz : le cylindre elliptique parallèle à Oy :  le cylindre hyperbolique parallèle à Ox : Biquadratique sphérique. Paramétrisation cartésienne : .

L'ellipse sphérique est l'ellipse géodésique sur la sphère, lieu des points dont la somme des distances (mesurées sur la sphère) à deux points fixes F, F' de la sphère est constante. Autrement dit, c'est le résultat du tracé du jardinier de l'ellipse plane classique transposé sur la sphère.
Si l'on prend les notations ci-dessus, il se trouve que le lieu des points vérifiant  est formé de l'ellipse précédente et de sa symétrique par rapport à xOy ; la réunion des deux ellipses peut donc être désignée par "hyperbole sphérique".
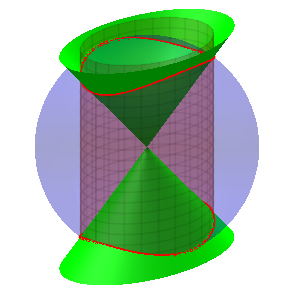
En utilisant les formules de trigonométrie sphérique, on montre que l'hyperbole sphérique est section de la sphère par un cylindre elliptique d'axe passant par le centre de la sphère. C'est donc un relèvement d'ellipse sur une sphère.
C'est donc aussi une courbe algébrique de degré 4, intersection de toutes les quadriques du faisceau engendré par la sphère et le cylindre (des représentants remarquables étant représentés ci-dessus).

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2014