ELLIPSE
Ellipse
(eng.)
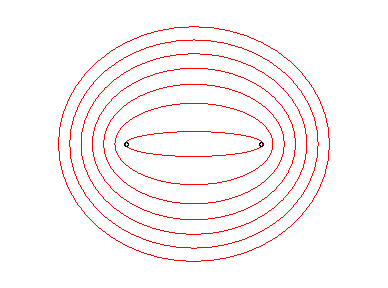
Nous conseillons au lecteur de lire cette page en parallèle
avec celle consacrée à l'hyperbole.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
ELLIPSE
Ellipse
(eng.)

Nous conseillons au lecteur de lire cette page en parallèle
avec celle consacrée à l'hyperbole.
| Du grec elleipein "manquer".
Nom donné par Apollonius de Perge. Voir sur cette page d'Alain Esculier les programmes de tracé des animations. |
 |
Équation cartésienne réduite : a = demi grand axe ³ b = demi petit axe > 0. F(c, 0) et F'(–c, 0) : foyers de l’ellipse. (D), (D'), droites d'équation K : pied de la directrice sur l'axe Ox. d = FK = |
| Paramétrisation cartésienne : Équation polaire : Équation podaire : Abscisse curviligne : Rayon de courbure : Équation bifocale : Équation polaire (pôle F, axe Ox) : Équations cartésienne et polaire dans un repère d’origine un sommet et d’axe des abscisses l’axe focal : Longueur, donnée par une intégrale elliptique de deuxième espèce : Rayon du disque de même aire : |
Les ellipses sont les coniques d'excentricité < 1.
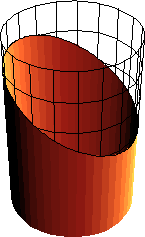
Elles ont été historiquement définies comme section de cône de révolution par un plan faisant avec l’axe du cône un angle supérieur à celui de l’angle entre une génératrice et l’axe :

ellipse = intersection bornée d'un cône et d'un plan |
Application : la trace d'un cône de lumière sur un mur a un contour elliptique, si elle est bornée |
mais plus généralement toute section bornée d’une quadrique par un plan est une ellipse.
L'ellipse possède de nombreuses définition géométriques planes :
1) Définition bifocale.
- l'ellipse est le lieu des points
dont la somme des distances à deux points fixes F et F'
est constante (voir l’équation bifocale) ; d'où les deux
constructions suivantes :
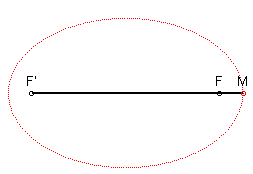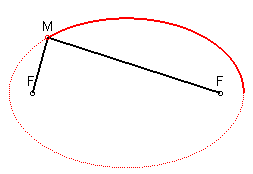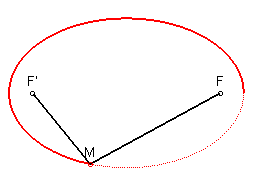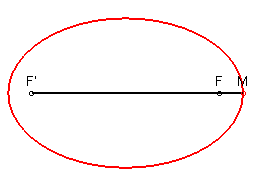 |
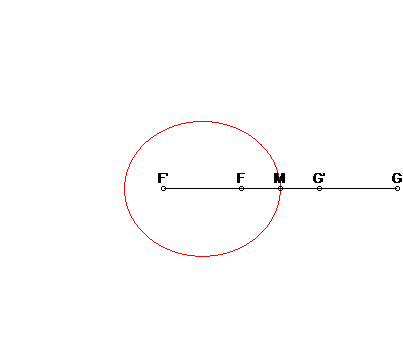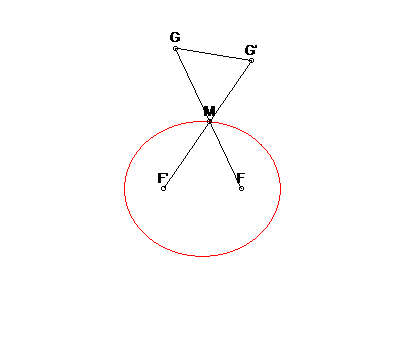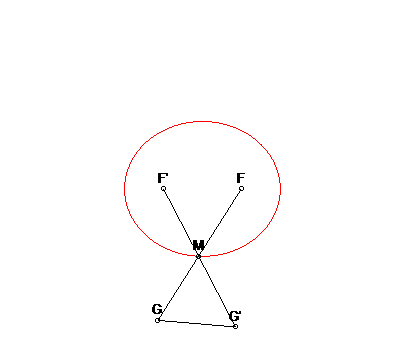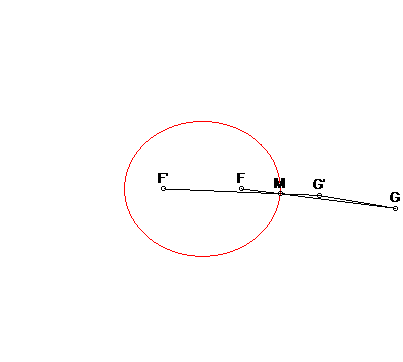 |
|
Voir à caustique inverse, une généralisation de cette construction. |
|
On peut aussi voir cette définition comme "lieu des points dont la distance moyenne à deux points est constante (égale à a)".
Application :  Entre les deux pylônes, ce téléphérique décrit
un arc d'ellipse.
Entre les deux pylônes, ce téléphérique décrit
un arc d'ellipse.
La construction des foyer et directrice de l'ellipse
définie comme section d'un cône est donnée par le théorème
de Dandelin illustré ci-dessous :
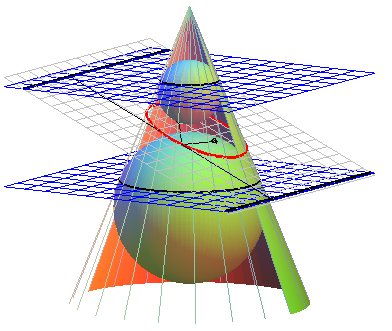 |
Les 2 sphères inscrites dans le cône et tangentes au plan de l'ellipse le sont aux foyers de celle-ci, et les plans des cercles de contact coupent le plan de l'ellipse en les 2 directrices. |
Pour une généralisation plane de la propriété
: , voir
les
ovales de Cayley et
les ovales de Descartes ; pour
une généralisation à l'espace, voir l'ellipse
sphérique.
1 bis) L'ellipse est le lieu d'un point M tel que la tangente en M à ce lieu est la bissectrice extérieure de l'angle F'MF :
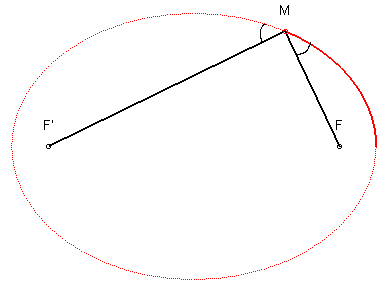
D'après les lois de la réflexion, tout rayon lumineux (ou toute onde sonore) issu(e) de F, est donc réfléchi(e) par l'ellipse suivant une droite passant par F'.
Applications :
|
Dans le métro parisien, deux personnes situées aux deux foyers de la voûte elliptique peuvent converser d'un quai à l'autre sans être entendues. Des salles de l’abbaye de La Chaise Dieu -pour confesser les lépreux- ont une propriété similaire. Des chuchotements à tel endroit sont clairement perçus en tel autre et pas ailleurs… Même chose au couvent du désert des lions près de Mexico (galerie des soupirs), au musée du Louvre, à la Cathédrale d'Agrigente en Sicile, etc.... |
 |
|

Dans ce billard elliptique, pour mettre la balle dans le trou après un rebond, il suffit de viser l'autre foyer (ce que ne fait pas la personne sur la photo !) |
Enceinte elliptique. |
| Autre application : en tout point M de l'ellipse
de départ, l'ellipse symétrique par rapport à la tangente
en M est l'ellipse de foyers les points G et G' vus
ci-dessus lors de la construction par trois-barres.
De plus, cette ellipse roule sans glisser sur la première. Note : le milieu de la bielle [GG'], centre de l'ellipse roulante décrit une courbe de Booth. |
 |
| Si l'on se place dans le plan lié à F' et G', les deux ellipses tournent autour de F' et G' en restant constamment tangentes, avec un roulement sans glissement : c'est la propriété d'isotrépence de l'ellipse par rapport à un foyer. |
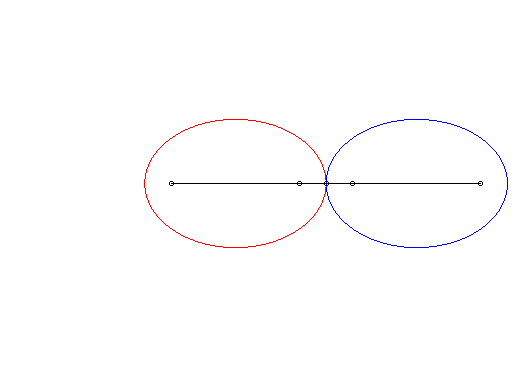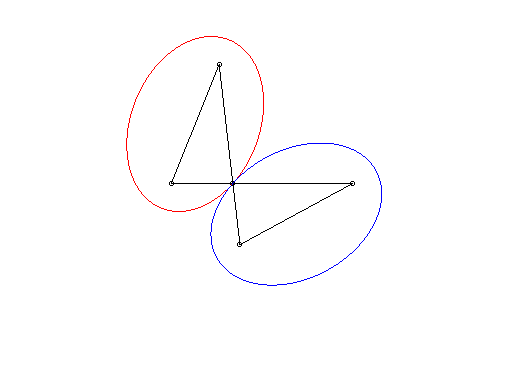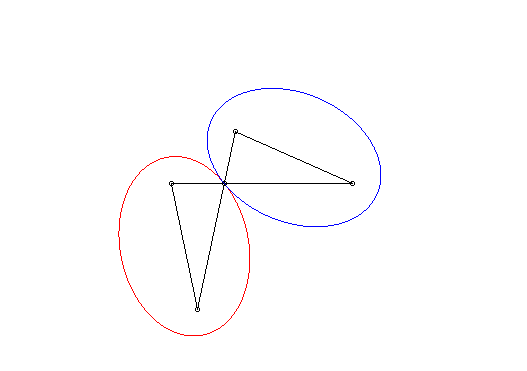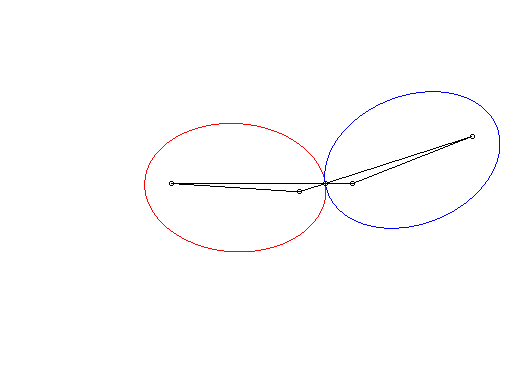 |
2) Définition par courbe
d'équidistance entre un point et un cercle, autrement dit comme
isotèle
de cercle.
L'ellipse est le lieu des points équidistants
d'un cercle (appelé cercle directeur, de centre l'un des foyers
F'
et de rayon 2a) et d'un point situé à l'intérieur
de ce cercle (qui est l'autre foyer F) ; autrement dit, c'est le
lieu du centre d’un cercle variable astreint à passer par F
et à être tangent à C(F', 2a)
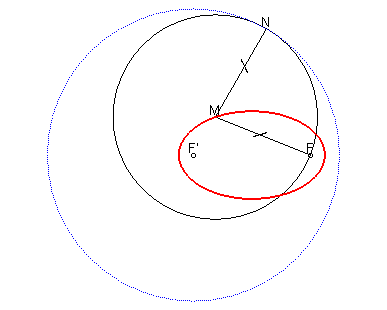
Plus généralement les courbes
d'équidistance entre deux cercles intérieurs sont des
réunions d'ellipses :
| Les points rouges sont les points "équidistants" du cercle bleu et du cercle vert | ||
 |
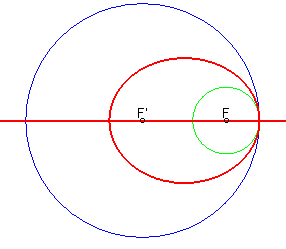 |

Lorsque les cercles sont sécants, la courbe d'équidistance est réunion d'une ellipse et d'une d'hyperbole. |
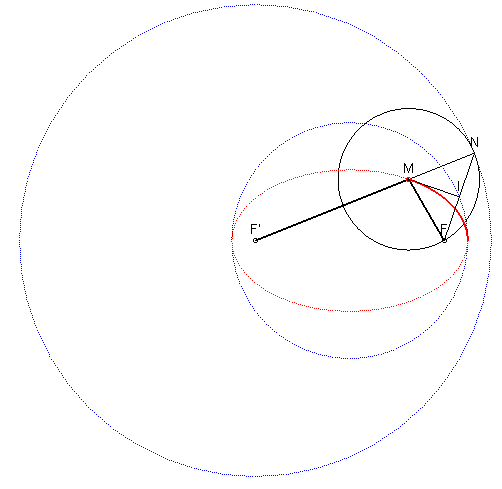
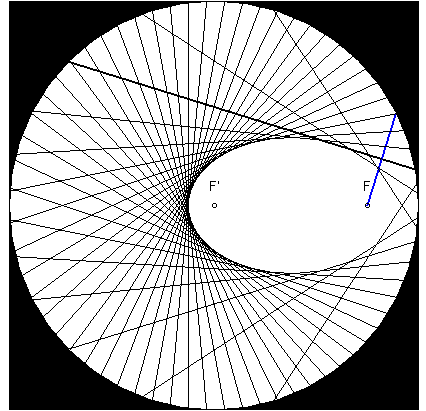
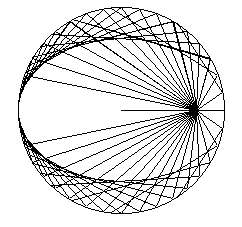
3) Définition tangentielle par antipodaire de cercle.
L'ellipse est l’enveloppe de la perpendiculaire en I
à la droite (FI), I décrivant le cercle principal
C(O, a) (autrement dit, l’antipodaire
de ce cercle par rapport à F), ou encore l’enveloppe de la
médiatrice du segment [FN], N décrivant le
cercle directeur C(F', 2a) (qui est donc l’orthotomique
de l’ellipse par rapport à F).
 |
 |
| Cette propriété est à la base de
la construction de l'ellipse à l'aide d'une équerre dont
l'angle droit décrit un cercle et un côté passe par
un point fixé.
Egalement à la base de l'élégante construction par système articulé présentée à droite. |
 |
 |
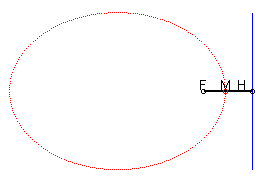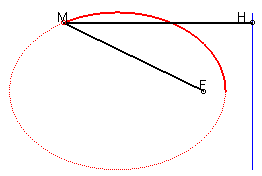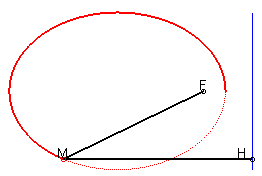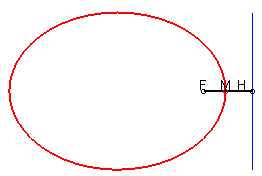
4) Définition par foyer et directrice (non valable
pour le cercle).
L'ellipse est le lieu d’un point M tel que
où H est le projeté de M sur la directrice
(D), avec e strictement compris entre 0 et 1.
4 bis)
L'ellipse est le lieu d'un point M tel que MF
+ eMH' = 2a où H' est le projeté de M
sur la directrice (D'), avec e strictement compris entre
0 et 1.
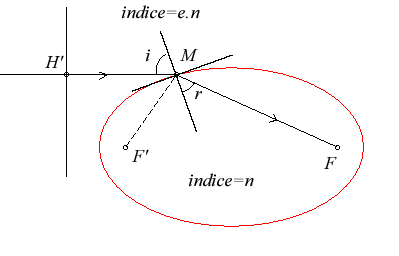
| Interprétant la quantité MF + eMH'
comme un chemin optique, cela signifie que si l'intérieur de l'ellipse
est constitué d'un milieu d'indice de réfraction n
et l'extérieur d'indice e.n, les rayons incidents parallèles
à l'axe de l'ellipse situés du côté de (D')
seront réfractés en des rayons passant tous par F.
En d'autres termes, la caustique par réfraction de l'ellipse pour des rayons parallèles à l'axe est réduite aux deux foyers. |
|
| Ceci a comme application la conception de lentilles convergentes (l'indice de réfraction de la lentille doit être égal à 1/e) : | 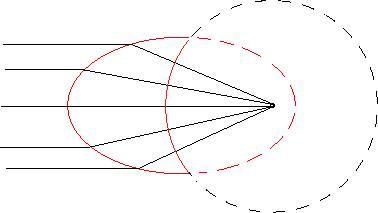 |
5) Définition par affinité de cercle.
L'ellipse est l’image par l'affinité
du cercle principal C(O, a) et aussi image par l'affinité
du cercle secondaire C(O, b), d'où la construction,
dite “par réduction d’ordonnée”, qui montre que l'ellipse
est la transformée
de Newton de 2 cercles concentriques :

Plus généralement, toute application affine
transforme un cercle en une ellipse ; en voici des applications :
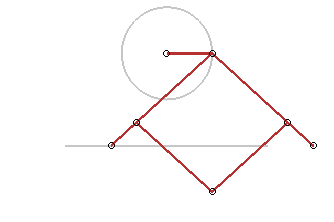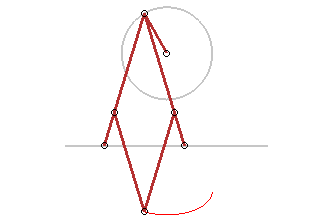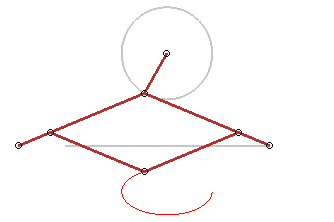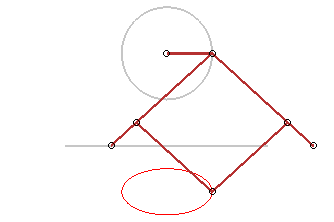 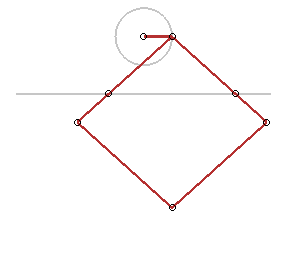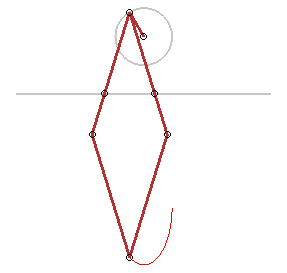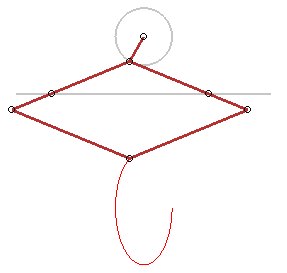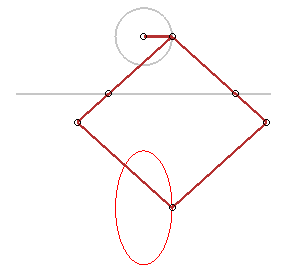
Trace-ellipse de Delaunay |
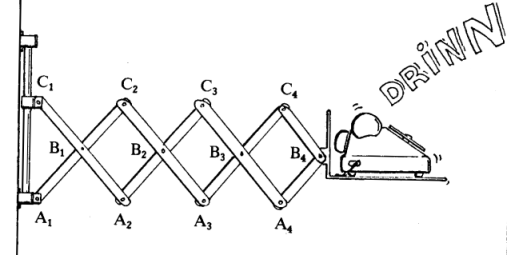 |
6) L'ellipse est le lieu d'un point d’un segment dont
les extrémités se déplacent sur des droites non parallèles
(et d'ailleurs de tout point lié à ce segment), d’où
la construction, dite “à la bande de papier” :
 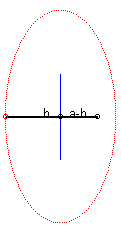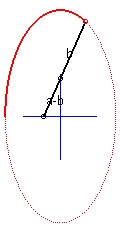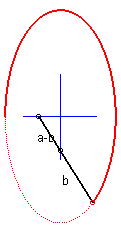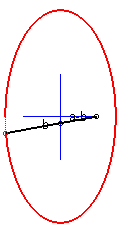
Par cette méthode, une même ellipse est obtenue de 2 façons différentes. Remarquons que la droite mobile enveloppe, elle, une astroïde. |

Trace-ellipse d'Archimède (ou de Proclus), utilisant cette propriété |
Toutes les roulettes du mouvement plan sur plan associé sont des ellipses ; voir à glissette.
Applications :
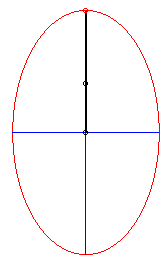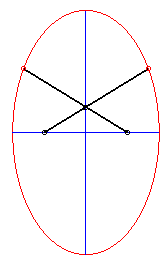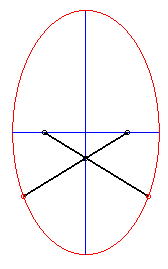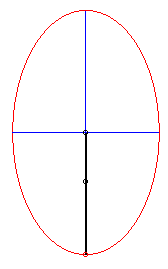
On ouvre des ciseaux en faisant glisser les extrémités sur une table ; les pointes décrivent une ellipse. |
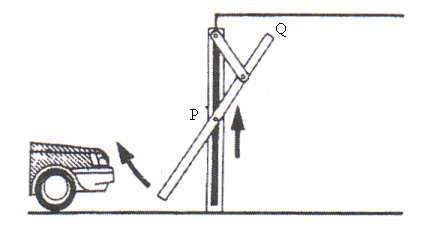
Les points P et Q décrivent deux droites perpendiculaires : |

D'où un autre trace-ellipse dit "de Van Schooten" (pouvant aussi être considéré comme une bielle de Bérard). |
Pour d'autres courbes obtenues par des mécanismes articulés, voir à courbe du trois-barres.
7) Définition trochoïdale.
|
L'ellipse est une hypotrochoïde, avec un cercle roulant de rayon moitié de celui du cercle de base (composition de deux mouvement circulaires de mêmes vitesses angulaires et de sens contraires). |
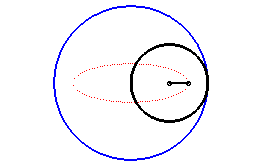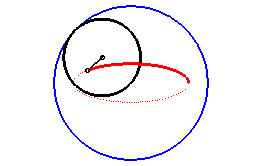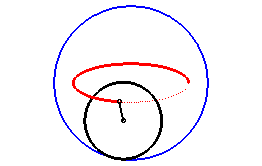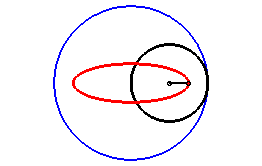 |
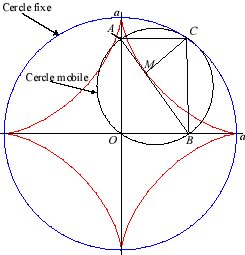
| Cette définition est en fait liée à la précédente, comme le montre cette figure ; le mouvement du plan lié au segment [A B] sur le plan fixe a pour base le cercle bleu et pour roulante le cercle noir de diamètre [A B], de rayon moitié ; tous les points du plan mobile décrivent des ellipses, les hypotrochoïdes précédentes, qui sont donc les roulettes de ce mouvement plan sur plan. |
 |
8) Définition par diamètres conjugués.
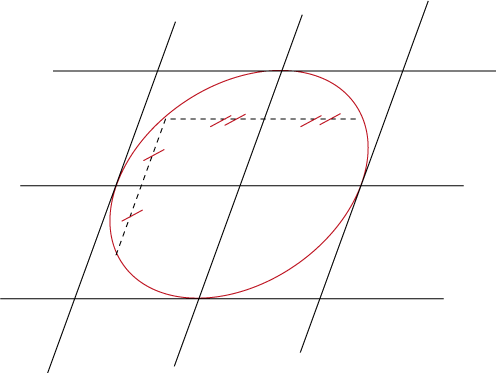
| Toute droite passant par le centre de l'ellipse (diamètre
de cette ellipse) est axe de symétrie OBLIQUE de l'ellipse,
la direction de la symétrie étant donnée par les tangentes
à l'intersection de l'axe avec l'ellipse. Le diamètre parallèle
à cette direction est lui aussi axe de symétrie oblique,
la direction étant parallèle au premier diamètre,
et les deux diamètres sont dits conjugués.
Réciproquement, tout convexe ayant des axes de symétrie oblique dans toutes les directions a pour bord une ellipse (BERGER th. 15.5.9). NB : dans la paramétrisation |
 |
9) L'ellipse est un cas particulier de courbe
de Lissajous.
_________________________________________________________________________________________________
|
Les cercles de courbure aux sommets se construisent très simplement, et permettent une construction approchée de l'ellipse : |
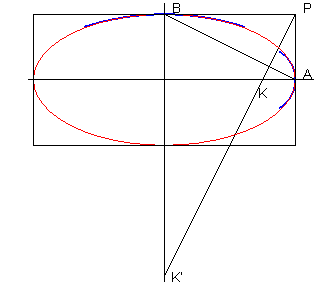
Les cercles bleus se construisent facilement ((KK') perpendiculaire à (AB)) |
Pour la développée de l'ellipse, voir à
tétracuspide
; les courbes parallèles à l'ellipse sont les toroïdes
; l'antipodaire de l'ellipse par rapport à son centre est la courbe
de Talbot.
Voir aussi sur cette
page le mouvement plan sur plan défini par une ellipse astreint
à passer par deux points fixes.
Voici encore un mécanisme, dit "de Cavalieri" pour
tracer les ellipses :  .
.
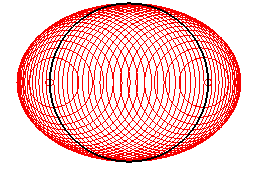 |
L'enveloppe des cercles dont le diamètre parallèle
à une direction donnée a ses extrémités sur
un cercle est l'ellipse dont les foyers sont diamétralement opposés
sur le cercle et tangente au cercle (coefficient d'aplatissement et excentricité
égaux à |

Pont en Bretagne (photo Mauricette Decamp) |

Le Colisée (qui a une forme elliptique approchée, pas seulement par perspective !) |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL Alain ESCULIER 2024