Ellipsoïde

ELLIPSOÏDE
Ellipsoid, Ellipsoide

Équation cartésienne réduite :

,
avec a (demi grand axe )

(demi axe moyen )

(demi petit axe) > 0.
Quand a = b ou b = c : ellipsoïde de révolution, ou sphéroïde (sinon, l'ellipsoïde est dit scalène).
     - quand a = b : ellipsoïde de révolution aplati (forme de galet ou de soucoupe volante)
     - quand b = c : ellipsoïde de révolution allongé (forme de ballon de rugby ou de cigare)
     - quand a = b = c : sphère.
Paramétrisations cartésiennes :
1)

.
2) coordonnées de Mercator, changer sin v en th v dans 1) :

.
3) coordonnées stéréographiques de pôle sud :

.
4) paramétrisation dont les lignes de coordonnées sont les lignes de courbure :

avec

; le cas u = v = b donne les 4 ombilics de coordonnées :

.
5) paramétrisation dont les lignes coordonnées sont les cercles de l'ellipsoïde :

Élément d’aire (avec la première paramétrisation) :

.
Courbure de Gauss :

où

est la distance de O au plan tangent au point considéré.
Courbure moyenne :

.
Rayons de courbure principaux :
- cas a > b > c, avec la paramétrisation ci-dessus par les lignes de courbure :

Aire, formule symétrique :.
Aire, formule pour a > b > c : où , sont les intégrales elliptiques de premières et seconde espèce, , .
Volume : .
Rayon de la boule sphérique de même volume : .

L’ellipsoïde peut être défini comme une quadrique bornée.

L’ellipsoïde est :
- l’image par la bidilatation de la sphère circonscrite S(O, a).

- le lieu d'un point fixe M d’une droite variable (D) dont 3 points fixes P,Q,R sont astreints à se déplacer chacun dans 3 plans fixes deux ) deux sécants ; les 3 demi-axes sont alors MP, MQ, MR.

Les plans de coordonnée xOy, yOz, zOx sont les plans principaux de l'ellipsoïde, et leurs sections avec l'ellipsoïde en sont les ellipses principales ; deux de ces ellipses suffisent pour définir l'ellipsoïde (et l'ellipsoïde est de révolution ssi l'une d'elles est un cercle) :

Les sections planes de l'ellipsoïde sont des ellipses, qui sont semblables quand les plans sont parallèles.
Quand l'ellipsoïde n'est pas de révolution, il existe deux directions de plans pour lesquelles ces sections sont circulaires, ce qui montre que l'ellipsoïde est une surface doublement cerclée (voir la paramétrisation 5) ci-dessus).

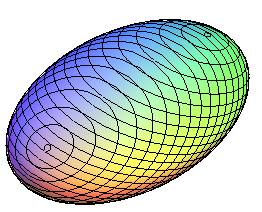
Les deux réseaux de cercles de l'ellipsoïde ; les 4 cercles limites sont les ombilics.
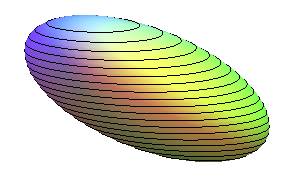
L'un des réseaux de cercles mis à l'horizontale.

La méthode de la Hire (ou de la bande de papier) pour construire l'ellipse se généralise comme suit à l'ellipsoïde : si 3 points fixes d'une droite (D) sont astreints à se mouvoir chacun dans trois plans deux à deux sécants, tout point de la droite (D) décrit un ellipsoïde ; par exemple, si une droite (D) coupe yOz en A , zOx en B et xOy en C et si M(x,y,z) de (D) est tel que MA = a, MB = b et MC = c, alors x²/a² + y²/b² + z²/b² = 1.

Voir les géodésiques de l'ellipsoïde sur Loria 3D Tome 2 p. 220.

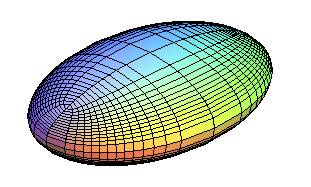
Lignes de courbure de l'ellipsoïde, dont les trois ellipses principales sont des cas particuliers ; les 4 points singuliers sont les ombilics.
Ce sont des "ellipses géodésiques" de foyers les ombilics (la somme des distances géodésiques aux ombilics est constante).

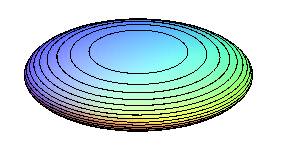
Ellipsoïde de révolution aplati ; il n'y a plus que deux ombilics.

Ellipsoïde de révolution allongé, même remarque.

Voir les ellipsoïdes de révolution sur une page spécifique.

Les dômes elliptiques sont, plus ou moins, des demi-ellipsoïdes.
Église San Carlo alle Quattro Fontane, Rome.

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres