GLISSETTE
Glissette,
Gleitkurve
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
GLISSETTE
Glissette,
Gleitkurve

| Notion étudiée par Catalan en 1865 et par
Besant
en 1869.
Voir [Brocard]. |
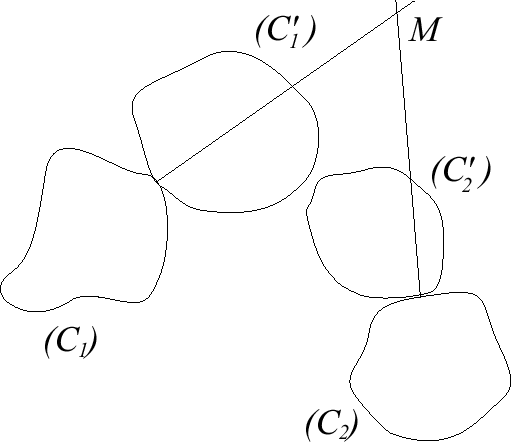
| Les glissettes sont des courbes tracées
dans un plan fixe par un point d'un plan mobile, le mouvement du plan mobile
étant obtenu par glissement de deux de ses courbes sur deux courbes
du plan fixe.
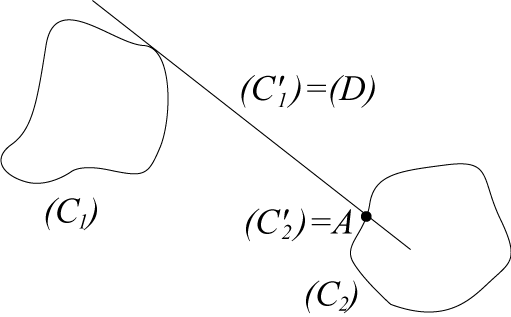
Plus précisément, soient (C1) et (C2) deux courbes d'un plan fixe (les bases), et (C '1) et (C '2) deux courbes d'un plan mobile (les glissantes) : le mouvement du plan mobile est déterminé par le fait que (C '1) reste tangente à (C1) et (C '2) à (C2) ; les glissettes associées sont les traces d'un point du plan mobile dans le plan fixe. Remarquons que tout mouvement
plan sur plan étant obtenu par roulement sans glissement d'une
roulante sur une base, toute glissette est en fait aussi une roulette.
On en déduit un beau théorème de
dualité : si l'on échange les bases et les glissantes (autrement
dit, on fixe (C '1) et (C '2)
et (C1) et (C2)
glissent respectivement sur elles), alors la base et la roulante du mouvement
plan sur plan s'échangent elles aussi.
|
 |
CAS PARTICULIER N° 1 (cas originel ayant donné lieu à la notion de glissette)
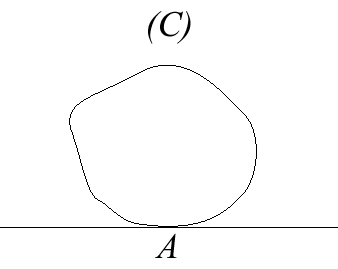
| Cas où (C1)
est une droite (D), (C2)
se réduit à un point A de la droite (D) , et
(C '1) et (C '2)
sont une même une courbe (C) ; le mouvement du plan mobile
est donc défini par le fait que la glissante (C) reste tangente
à la droite (D) au point A.
Le centre instantané de rotation de ce mouvement plan sur plan est le centre de courbure en A ; la roulante est la développée de (C) qui roule sans glisser sur la base, qui est la normale en A. On en déduit que les glissettes à base rectiligne d'une courbe sont les roulettes à base rectiligne de la développée de cette courbe. Dans ce cas, on obtient les formules suivantes : |
 |
| Si la glissante à pour paramétrisation
cartésienne dans le plan mobile la glissette du centre du repère a pour paramétrisation : la paramétrisation de la glissante à l'instant t est alors : Si la glissante a pour équation polaire la glissette du pôle a pour paramétrisation polaire : Inversement, si la glissette a pour équation polaire la glissante a pour paramétrisation polaire |
Exemples (voir aussi les roulettes
à base rectiligne, vu le théorème ci-dessus).
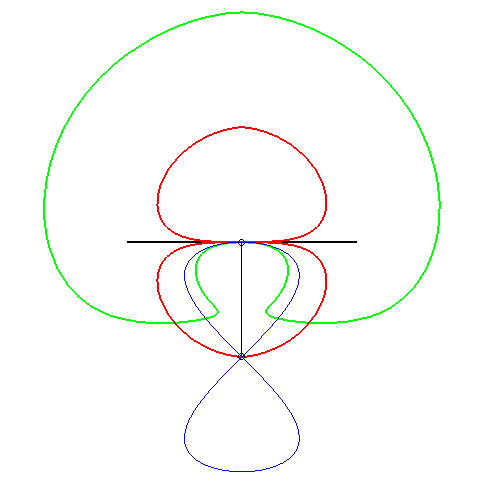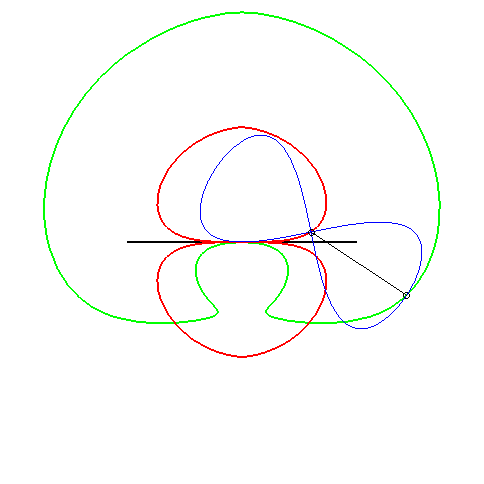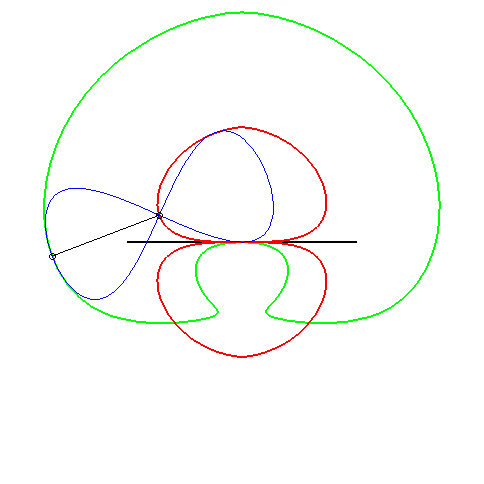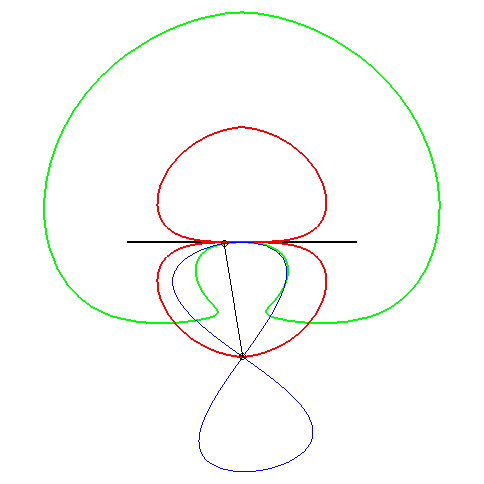
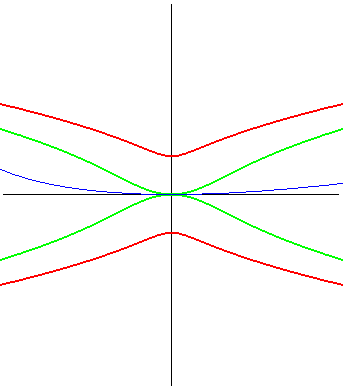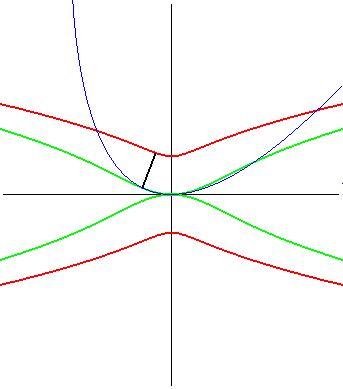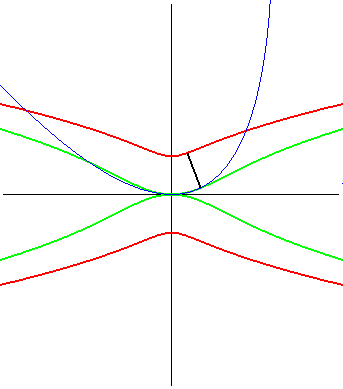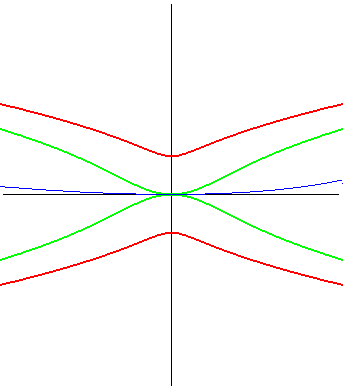
| (1) La glissette du foyer d'une parabole est une campyle
d'Eudoxe ; (2) celle du sommet (en vert ci-contre) est la courbe de
paramétrisation :
d'équation : |
 |
| (3) La glissette du centre d'une ellipse est une quartique
de Bernoulli de paramétrisation La glissette des foyers est la sextique (4) La glissette du centre d'une hyperbole équilatère est la courbe de Clairaut r² sin q = a². |
 |
| (5) La glissette de la pointe d'une cardioïde
est un oeuf double.
|
(6) La glissette du centre d'une lemniscate
de Bernoulli est une courbe du dipôle.
|
(7) La glissette du pôle d'une développante
de cercle est une droite (normal puisque la roulette du centre
d'un cercle (développée de la développante) roulant
sur une droite est une droite !)
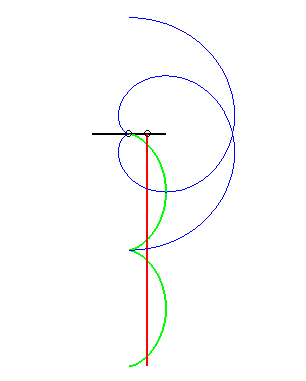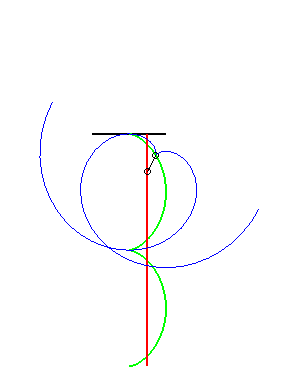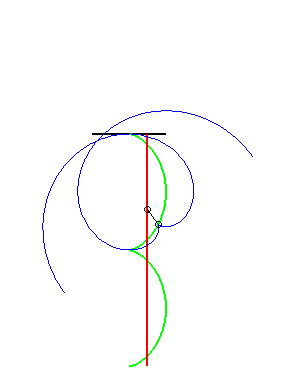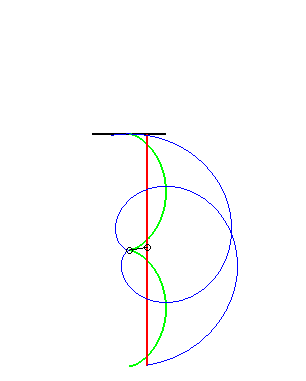 |
(8) Idem pour la glissette du pôle d'une spirale
logarithmique (c'est une conséquence du fait que l'angle
entre la tangente et le rayon vecteur est constant).
Les autres glisssettes sont des trochoïdes. 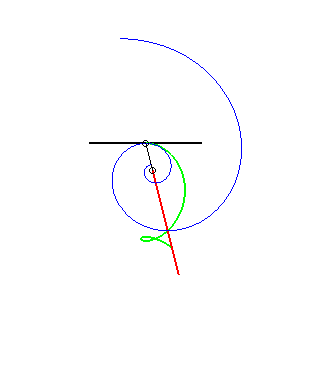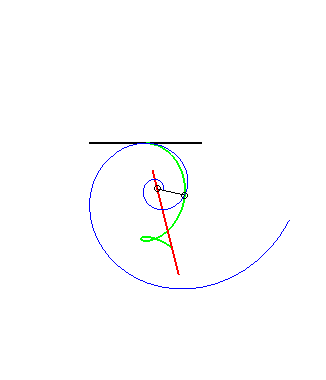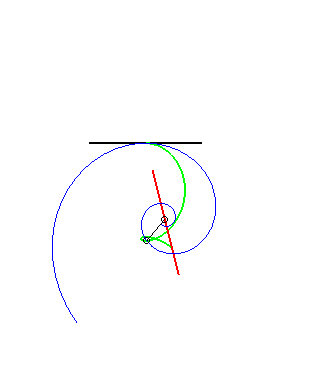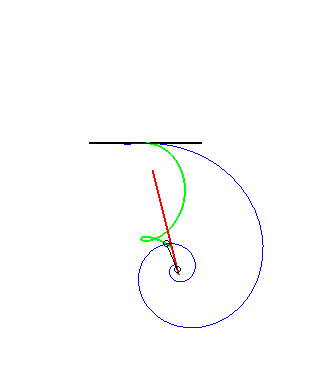 |
(9) La glissette du pôle d'une spirale d'Archimède
est un kappa.
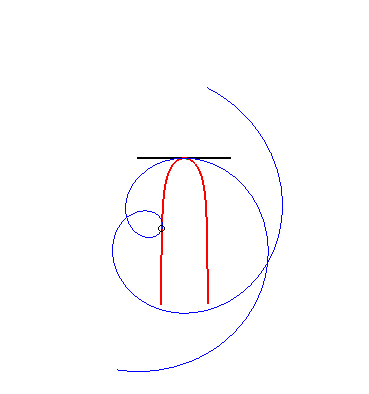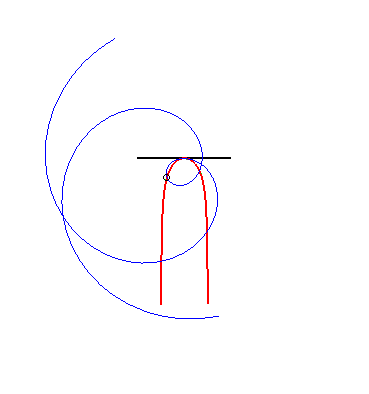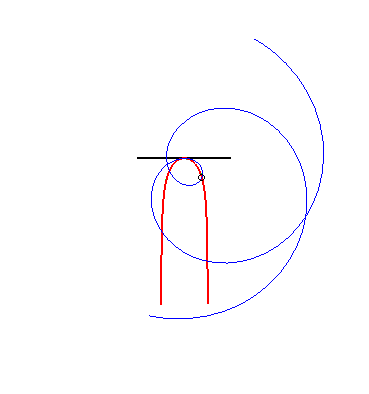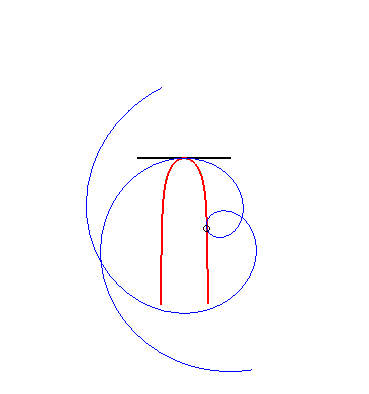 |
(10) Idem pour la glissette du pôle d'une spirale
hyperbolique.
|
Derniers exemples : les glissettes du centre du cercle fixe d'une
cycloïde à centre sont des ellipses (puisqu'il en est de
même pour leur roulettes).
La glissette du pôle d'une spirale
tractrice est un cercle.
CAS DUAL DU CAS N° 1
| Cas où une droite glisse sur une courbe fixe (C),
le point de tangence
A étant fixe sur la droite.
La glissette engendrée par un point de la droite glissante est alors une courbe équitangentielle associée à la courbe (C). Et la glissette engendrée par un point se projetant orthogonalement en A sur la droite n'est autre qu'une parallèle à la courbe (C). La base du mouvement plan sur plan associé est la développée de (C) et la roulante la normale en A. |
CAS PARTICULIER N°2
| Cas où (C1)
et (C2) sont réduits à
des points A et B , et (C'1)
et (C'2) sont comme précédemment
une même une courbe (C) ; ci-contre l'exemple de la glissette
du sommet d'une parabole passant par deux points fixes.
Lorsque B tend rectilignement vers A, ce cas "tend" vers le cas n° 1. Le cas dual est celui où le plan mobile est emmené par deux de ses points décrivant une même courbe fixe (C), voir à courbe de Holditch, et sur cette page, différents exemples où (C) est une conique. |
 |
CAS PARTICULIER N°3
Autres exemples où les courbes (C'1)
et (C'2) sont toujours une même
une courbe (C) :
| 1) Les deux courbes (C1) et (C2) sont des droites perpendiculaires : | |
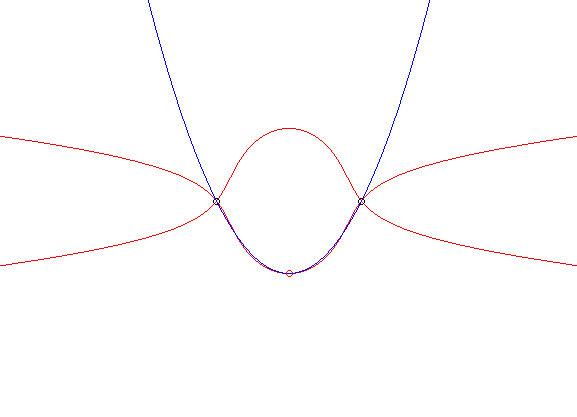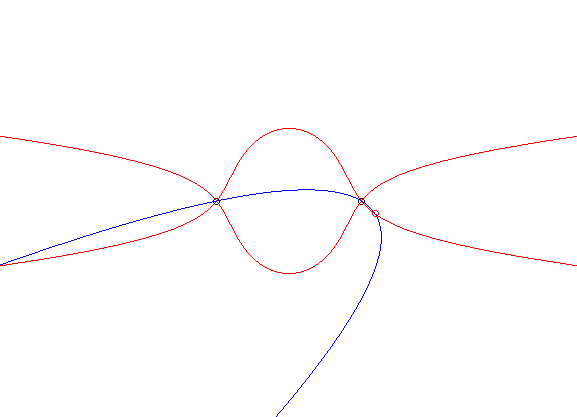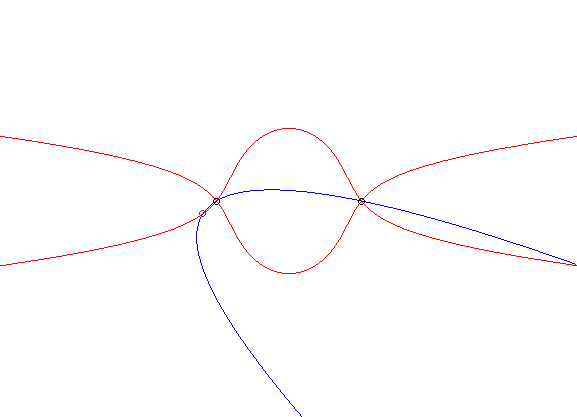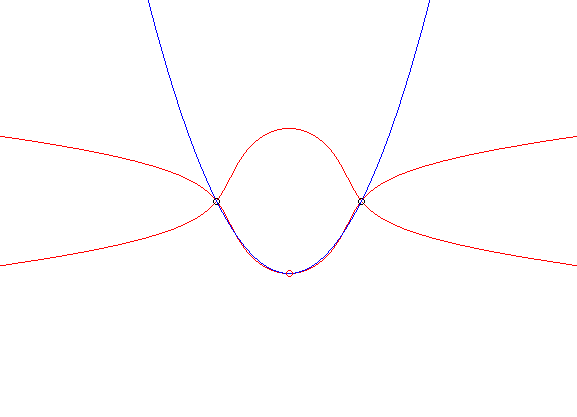
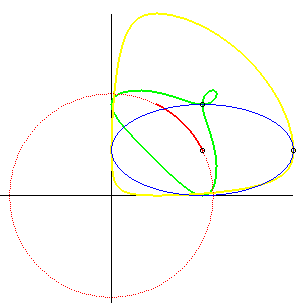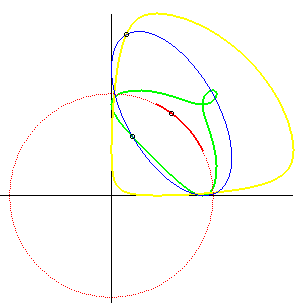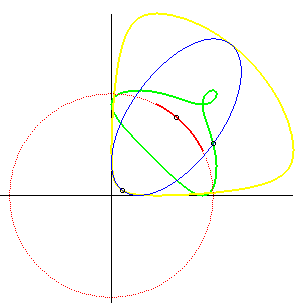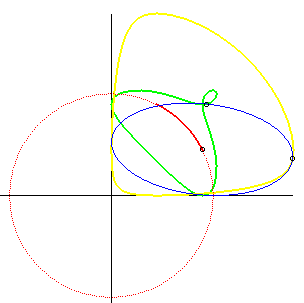
| Si une ellipse est astreinte à rester tangente
à deux droites perpendiculaires fixes, la glissette du centre de
l'ellipse est un arc de cercle (propriété inverse du fait
que la courbe orthoptique de
l'ellipse est un cercle).
Ci-contre nous avons ajouté les glissettes des sommets de l'ellipse. La glissette générale a pour paramétrisation : Pour l'étude complète, voir cette thèse p. 30. Cf aussi cette animation, montrant un système articulé très simple fournissant le mouvement de l'ellipse. |
 |
| Idem pour la parabole :
- la glissette du foyer de cette parabole est alors une cruciforme - celle du sommet (en vert ci-contre) est la courbe de paramétrisation : - celle du symétrique du sommet par rapport à l'axe est le moulin à vent (voir Aubert et Papelier tome 2 n° 317) Pour la base et la roulante, voir Besant p. 50. |
 |
| Dans le cas dual, la glissette du point d'intersection de 2 droites perpendiculaires tangentes à une même courbe n'est autre que la courbe orthoptique. |
| 2) La courbe (C1)
est une droite et (C2) un point
non situé sur cette droite.
Exemple de la glissette du sommet d'une parabole : |
 |
CAS PARTICULIER N°4
Les courbes (C'1)
et (C'2) sont réduites à
des points comme dans le cas n°2), mais (C1)
et (C2) sont distinctes : le plan
mobile se visualise bien par le mouvement d'une planche ayant deux roulettes
amovibles roulant sur deux rails.
Exemples :
| Cas où les courbes (C1)
et (C2) sont des droites perpendiculaires
: les glissettes sont des ellipses
; on retrouve ici la construction de l'ellipse par la méthode dite
de la bande de papier.
De plus la base du mouvement plan sur plan est un cercle, et la roulante un cercle de rayon moitié ; les points de cette roulante décrivent des segments de droite : on retrouve ici le dispositif de La Hire. Lorsque les deux droites sont non perpendiculaires, les glissettes sont toujours des ellipses (résultat de Léonard de Vinci [dictionnaire Penguin des curiosités géométriques p. 71] ). |
 |
|
| Si deux points du plan mobile coulissent sur deux cercles, les glissettes sont les courbes du trois-barres. |
 |
Lorsqu'une courbe est une droite et l'autre un cercle, on obtient les courbes de la bielle de Bérard et plus généralement lorsque l'une est une droite et l'autre une conique, on obtient les courbes polyzomales. |
CAS DUAL DU CAS N°4
(C1) et (C2)
sont réduites à des points fixes M1
et M2 , et les deux courbes (C'1)
et (C'2) sont astreintes à
passer par M1 et M2
.
| Cas où (C'1)
et (C'2) sont deux droites perpendiculaires.
Leur point d'intersection S décrit le cercle de diamètre
[M1M2].
Les points de la droite (M1S) restent à distance constante de S, donc décrivent une « conchoïde » du cercle décrit par S, de pôle M1 , qui appartient à ce cercle. Il s’agit d’un limaçon de Pascal. Nous laissons le lecteur comprendre d’après la figure la construction de la base et de la roulante qui sont, comme prévu par dualité, un cercle et un cercle de rayon double, le premier cercle étant justement celui décrit par S. Ceci permet de voir que toutes les glissettes sont des limaçons de Pascal. |
 |
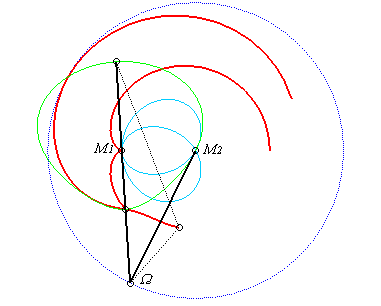
| Cas où (C'1)
et (C'2) sont respectivement une
droite et un cercle centré sur cette droite.
Il faut placer une barre double fixée en M2 et articulée en Les glissettes de points qui sont sur la deuxième branche tracent des « conchoïdes » du cercle lieu des points |
 |
CAS PARTICULIER N°5
| (C'1) et (C2) sont réduits à des points ; autrement dit, une courbe (Cm) du plan mobile passe par un point fixe Af , et un point Am du plan mobile décrit une courbe fixe (Cf). Notons qu'alors, le cas dual est du même type. | |
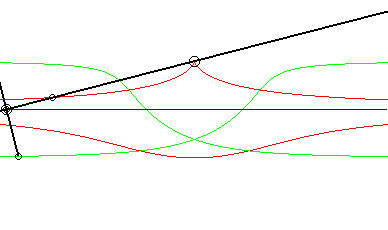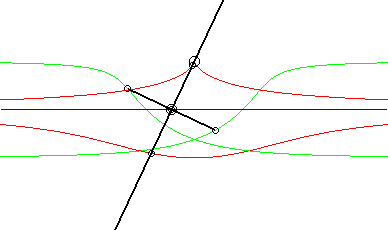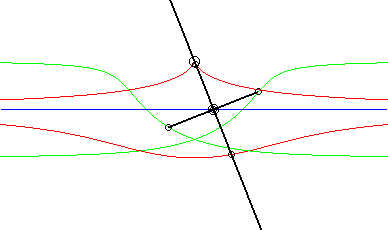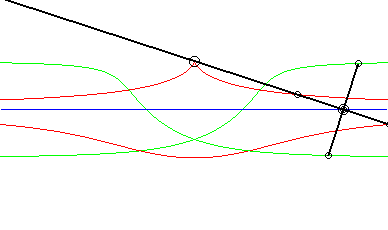
| Si la courbe mobile est une droite et le point mobile
est situé sur cette droite, les glissettes des points de la droite
mobile ne sont autres que les conchoïdes
de la courbe fixe par rapport au point fixe. Les autres en sont des isoconchoïdes.
Ci-contre, le cas où la courbe fixe est aussi une droite. On reconnaît bien en rouge une conchoïde de Nicomède ; en vert, deux isoconchoïdes. Le mouvement plan sur plan associé, appelé mouvement conchoïdal, est étudié sur cette page. |
 |
| Dans le cas dual, la courbe fixe est une droite et le
point fixe est sur cette droite ; la courbe mobile passe par ce point et
le point mobile décrit la droite.
Ci-contre, le cas où la courbe fixe est aussi une droite. La glissette du projeté du point mobile sur la droite mobile est un kappa (en gras), d'où le nom du mouvement plan sur plan associé : mouvement du kappa (voir cette page). Les autres glissettes sont des conchoïdes, ou des
isoconchoïdes de kappa par rapport à son centre.
|
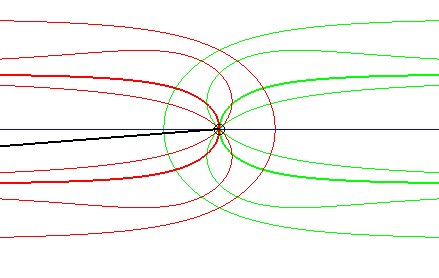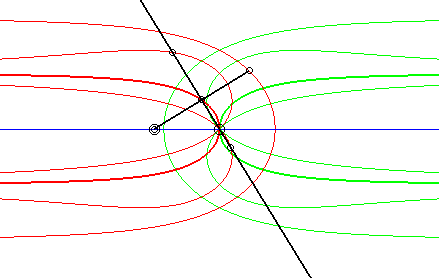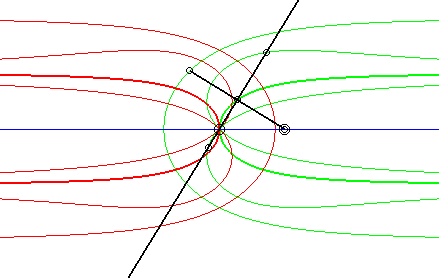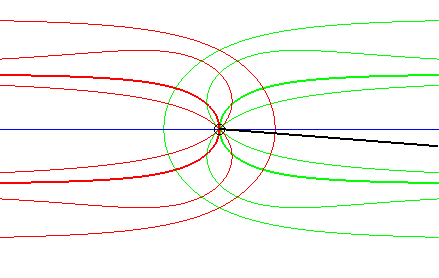 |
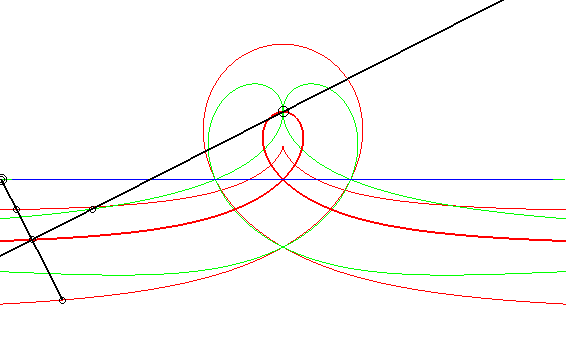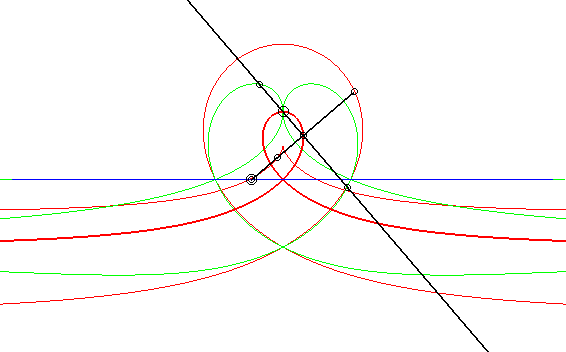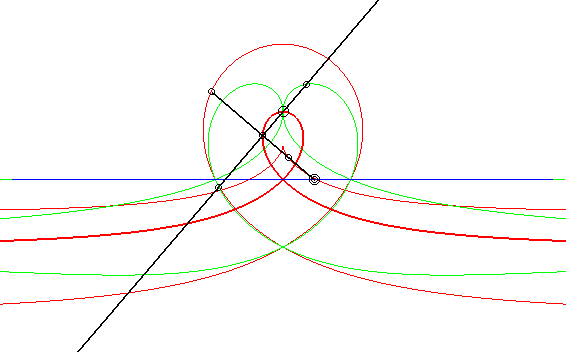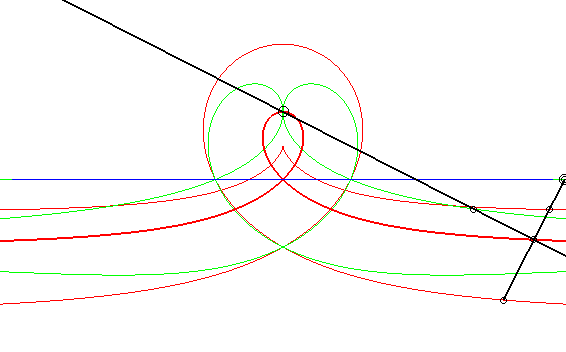
| Cas où les courbes fixe et mobile sont des droites,
les points fixe et mobile étant à même distance de
leur droite associée.
Les glissettes des points de la droite passant par le point mobile et perpendiculaire à la droite mobile sont les cubiques circulaires rationnelles droites. On retrouve ici le mécanisme dit de "l'équerre de Newton" pour tracer ces cubiques. En particulier, la glissette du projeté du point mobile sur la droite mobile est une strophoïde droite (en gras ci-contre). Les deux autres courbes rouges sont la cissoïde droite et la trisectrice de Maclaurin. Les glissettes des points de la droite mobile sont les conchoïdes de strophoïde droite par rapport à son sommet, c'est-à-dire les strophoïdes quelconques (deux exemples en vert ci-contre). Les autres glissettes sont des isoconchoïdes de la
strophoïde droite par rapport à son sommet.
|
 |
CAS PARTICULIER N°6
| (C'1) est une
droite (D), et (C'2) est
un point A de cette droite.
Autrement dit, un point A d'une bielle (D) est astreint à se déplacer sur une courbe (C2) tout en restant tangent à une courbe (C1). |
 |
| Exemple: (C1)
est un cercle de rayon a et (C2)
est une tangente à ce cercle.
On regarde la glissette d'un point de la bielle situé à une distance b de A. Paramétrisation : Eq. cartésienne : La base du mouvement plan sur plan est la parabole de foyer le centre du cercle et de directrice la tangente fixe et la roulante est la parabole de foyer A et de directrice la parallèle à la tangente mobile passant par le centre du cercle. |
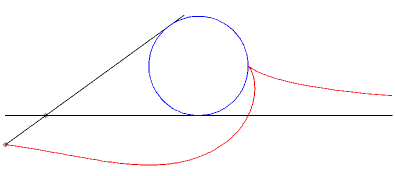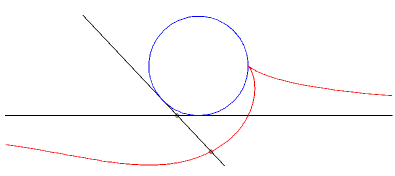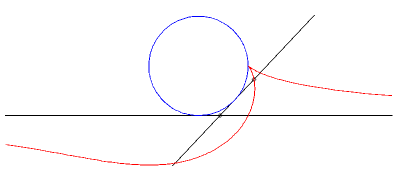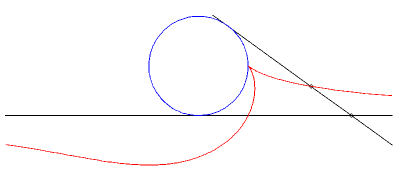
Cas a = b : cubique rationnelle cuspidale. |
CAS PARTICULIER N°7
| Les 4 courbes (C1)
et (C2), (C'1)
et (C'2) sont des cercles.
Les glissettes ne sont autres que de nouveau les courbes du trois-barres. |
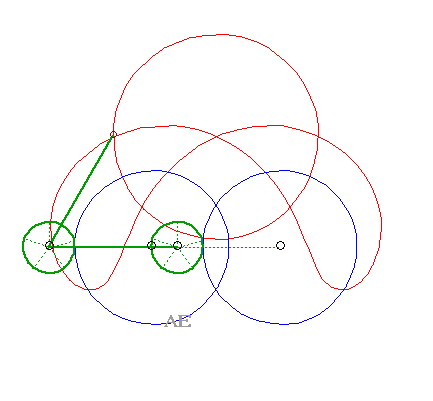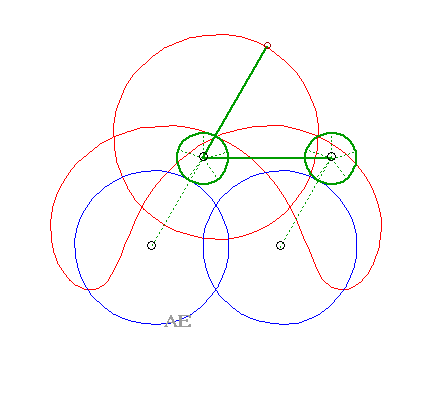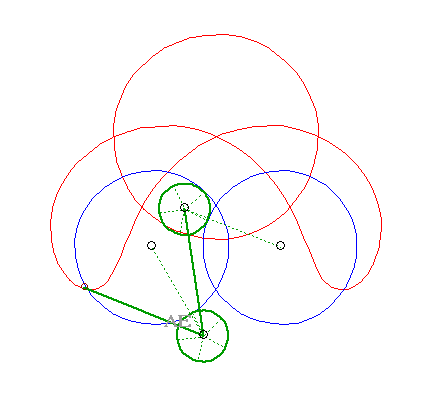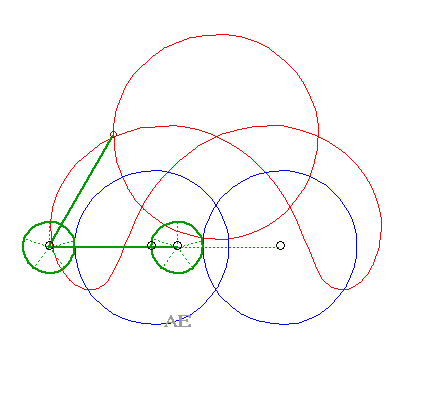 |
Une généralisation possible est de rajouter
une contrainte, mais d'autoriser que le plan mobile soit seulement semblable
au plan fixe, et non plus isométrique.
Exemples :
| Si le foyer d'une parabole est fixe, et la parabole astreinte à passer par un point fixe, la glissette du sommet de cette parabole est une cardioïde : |  |
| Inversement, si le sommet d'une parabole est fixe, et la parabole astreinte à passer par un point fixe, la glissette du foyer de cette parabole est une cissoïde droite : | 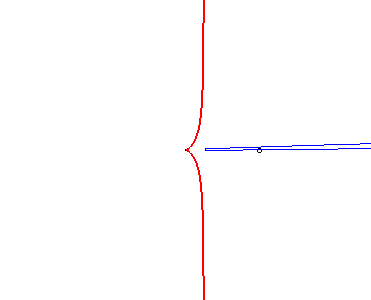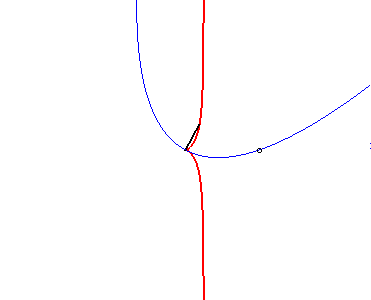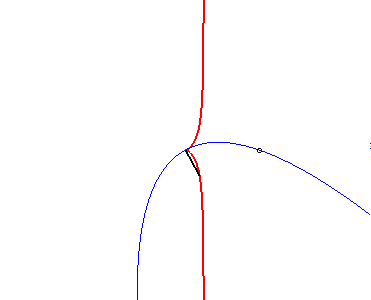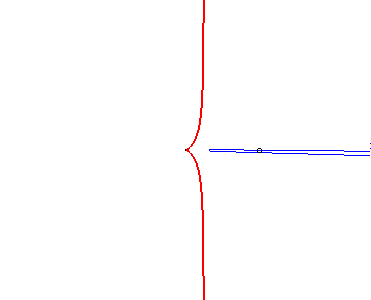 |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL , Alain ESCULIER 2022