COURBE PARALLÈLE À UNE AUTRE
Parallel
curve (or offset) of a curve, Parallelkurve

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE PARALLÈLE À UNE AUTRE
Parallel
curve (or offset) of a curve, Parallelkurve

| Notion étudiée par Leibniz en 1692.
Autre nom : courbe équidistante (à ne pas confondre avec la courbe d'équidistance). |
| Les courbes Pour une courbe de départ : Paramétrisation cartésienne : Les courbes parallèles à une courbe algébrique sont algébriques. Abscisse curviligne au point courant de 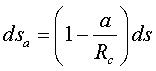 . .
Rayon de courbure : La longueur d'un arc de L'aire de la bande comprise entre deux arcs correspondants de |
Deux courbes sont dites parallèles si toute normale à l'une est une normale à l'autre ; on montre qu'alors la distance entre deux points à normale commune est une constante, appelée distance de parallélisme ; ne pas confondre avec des courbes translatées l'une de l'autre.
Deux courbes sont donc parallèles si ce sont les lieux des extrémités d'un segment de longueur constante se déplaçant toujours orthogonalement à sa direction, ce qui équivaut à ce que la droite portant ce segment roule sans glisser sur son enveloppe.
Voir aussi à reptoire la génération des parallèles par reptation d'un cercle sur une courbe.
Comme pour les droites, la relation de parallélisme
des courbes planes est une relation d'équivalence.
Une classe d'équivalence est l'ensemble des trajectoires
des points liés à une droite qui roule sans glisser sur une
courbe ; la droite mobile est la normale commune à toutes les parallèles,
et la droite fixe la développée
commune à toutes ces courbes.
Les courbes parallèles à un courbe sont
donc les développantes
de sa développée.
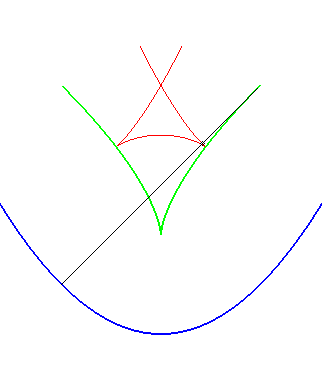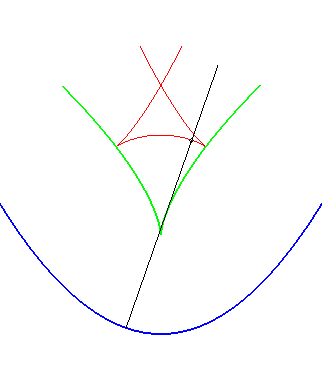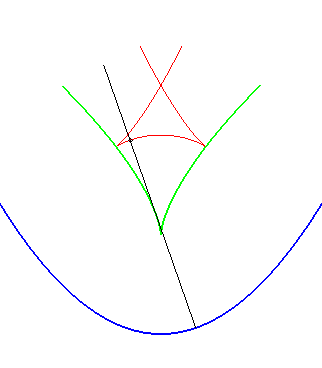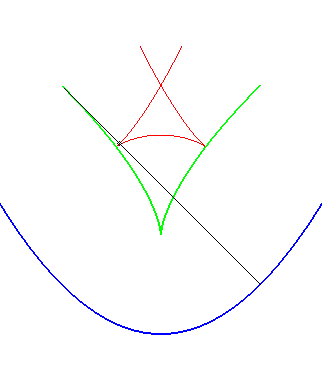
| La développante présentant (en général)
un rebroussement en un point de la courbe de départ, la développée
apparait comme le lieu des points de rebroussement des courbes parallèles.
Ci-contre, animation d'une normale roulant sans glisser sur la développée, traçant une parallèle à rebroussement (en rouge), qui est une des développantes de la développée (en vert). |
 |
Les courbes parallèles à une courbe
sont les courbes
,
parallèle d'indice a à
,
obtenues en reportant algébriquement une "longueur" a à
partir des points de
sur la normale orientée, autrement dit le lieu des points M
=
où
est le vecteur normal en M0
; Il s'agit donc d'un cas particulier de glissette
tangentielle.
a relation de parallélisme étant symétrique,
est aussi parallèle à
.
La réunion de
et
est
l' enveloppe des cercles de
rayon a centrés sur
; c'est donc aussi le contour apparent de la projection d'un tube
dont l'âme se projette suivant
.
Si l'on place la courbe
dans un plan ayant un mouvement de translation
circulaire de rayon a par rapport à un plan fixe, l'enveloppe
dans le plan fixe est de nouveau la réunion de
et
.
On peut voir les courbes parallèles à une
courbe ,
comme les courbes de niveau planes d'une surface
d'égale pente ayant
pour directrice.
Interprétation physique : la courbe
étant une source lumineuse, d'après le principe de Huygens,
les "fronts d’ondes" sont les enveloppes des ondelettes élémentaires
circulaires émises par tous les points de la courbe
; ce sont donc exactement les courbes parallèles à
.
Les points singuliers des courbes parallèles décrivant la développée de la courbe de base, avec l'interprétation physique précédente, la développée représente donc le lieu où sont concentrés les rayons lumineux émis par la courbe lumineuse.
Exemples :
- les courbes parallèles à
une droite sont les droites parallèles à cette droite (!)
- les développantes
d'une courbe sont parallèles entre elles.
- les toroïdes
sont les courbes parallèles à l'ellipse
- la sextique
de Cayley est l'une des courbes parallèles à la néphroïde
- les courbes parallèles à
la parabole x² = 2p y sont les courbes de paramétrisation
:
| Ci-contre, illustration de la construction des deux parallèles à distance donnée à la parabole, par enveloppe d'un cercle dont le centre décrit la parabole (non tracée sur les figures), ou par enveloppe des "translatées circulaires" de la parabole. | 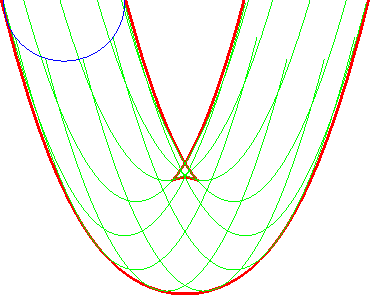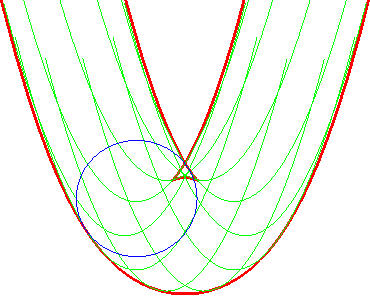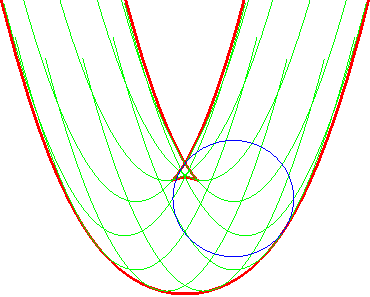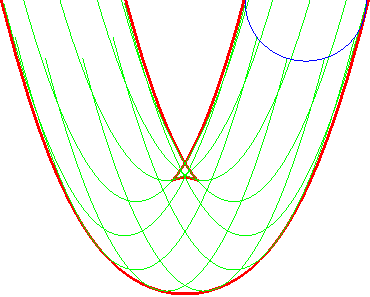 |
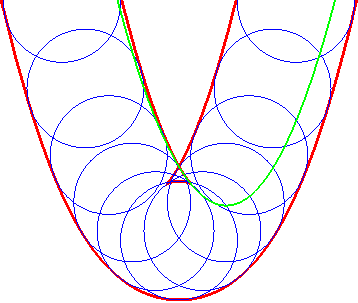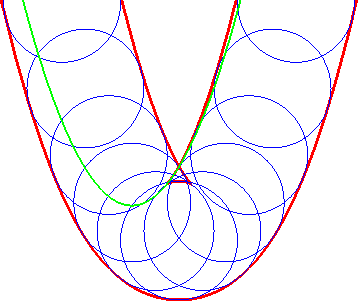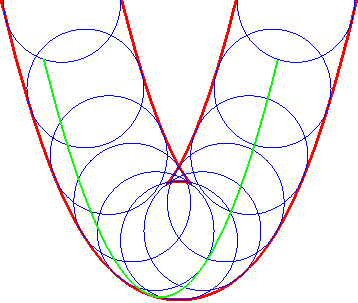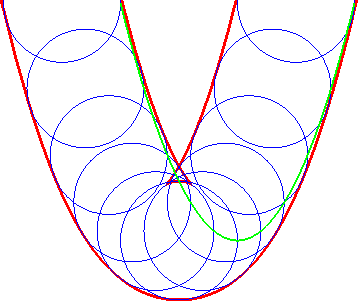 |
- Il peut arriver que les courbes
et
soient
égales ; la courbe
est alors parallèle à elle-même avec une distance 2
a.
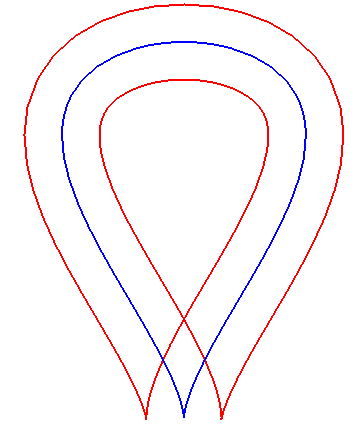 |
La courbe rouge est parallèle de deux façons à la courbe bleue, et auto-parallèle. |
Une notion voisine est la notion de courbe de niveau de la fonction "distance (d'un point du plan) à la courbe", appelée courbe (ou ligne) de distance. Ces courbes de niveaux sont formées de portions de courbes parallèles et d'arcs de cercles, et présentent l'intérêt de constituer une partition du plan, contrairement aux courbes parallèles.
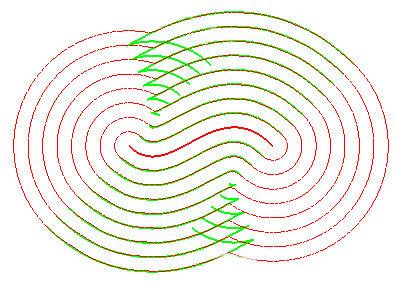
En vert les courbes parallèles, et en rouge, les courbes de
niveau de la fonction distance à la courbe ; lorsque ces dernières
ne se superposent pas à la courbe parallèle, ce sont des
arcs de cercle.
Les courbes parallèles sont des cas particuliers
de glissettes
tangentielles.
Voir aussi les courbes
parallèles en 3D et les surfaces
parallèles.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2019