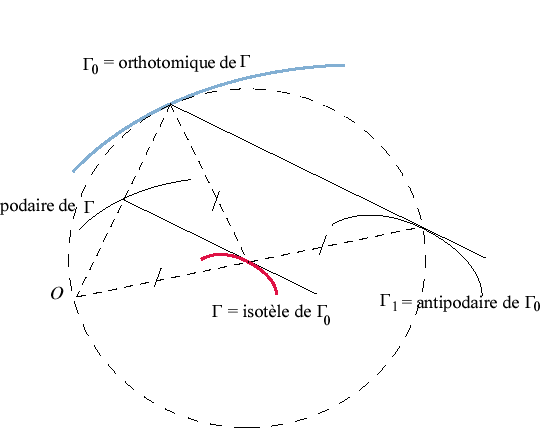
L'orthotomique étant l'image de la podaire dans une homothétie de centre O et de rapport 2, l'isotèle n'est donc autre que l'image de l'antipodaire dans une homothétie de centre O et de rapport 1/2 ; la notion est donc tombée en désuétude.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE ISOTÈLE
Isotel
curve, isotele Kurve
| Notion étudiée par Lepiney en 1909.
Du grec iso "même" et têle "loin". |
| La courbe isotèle d'une courbe plane L'orthotomique étant l'image de la podaire dans une homothétie de centre O et de rapport 2, l'isotèle n'est donc autre que l'image de l'antipodaire dans une homothétie de centre O et de rapport 1/2 ; la notion est donc tombée en désuétude. |
 |
Conclusion : à homothétie près, isotèle = antipodaire = orthocaustique.
Exemples :
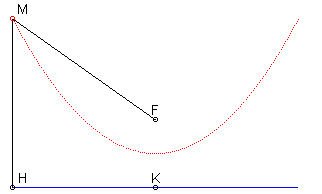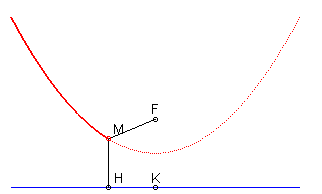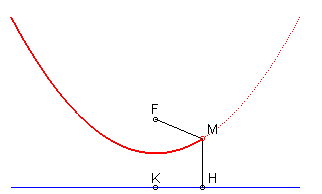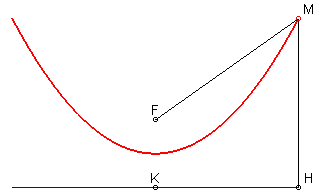
- la parabole est l'isotèle de sa directrice par rapport à son foyer.
- une conique à centre est l'isotèle du cercle directeur centré en un foyer par rapport à l'autre foyer.
- la courbe isotèle de l'ellipse par rapport à son centre est la courbe de Talbot.
Pour d'autres exemples, on se reportera à l'article
antipodaire.
| L'isotèle par rapport à O d'une
courbe
de largeur constante possède une propriété remarquable
découverte par Euler (Nova Acta Eruditorum, 1746) : tout
rayon issu de O réfléchi deux fois par l'isotèle
repasse par O. Euler désigne par catoptrice une courbe
ayant cette propriété.
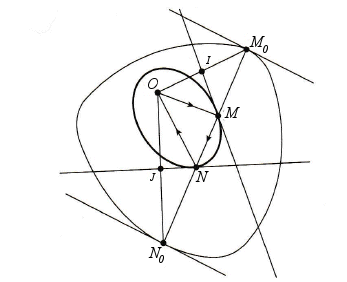
Le lecteur constatera sur la figure que le rayon issu de O se réfléchit bien en M suivant MN, puis en N suivant NO. De plus, comme OM+MN+NO=M0M+MN+NN0=M0N0, la distance parcourue par le rayon OMNO est constante égale à la largeur de la courbe de départ. |
 |
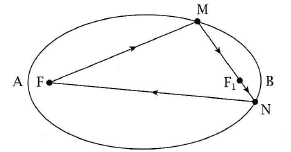
| Le cas de l'isotèle d'un cercle, qui est une ellipse de foyer O est un cas évident de cette propriété puisque tout rayon issu d'un foyer se réfléchit en un rayon passant par l'autre foyer. |
 |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2020