Courbe étudiée par Wallis en 1685, Peck en 1700, Bernoulli en 1726, Cesaro en 1878 et Falkenburg en 1884. Sous sa forme latine cochlea, le nom est dû à Wallis, et sous sa forme actuelle, à Falkenburg. Le terme latin cochlea est issu du grec kokhlias : coquille, limaçon (cf. la cochlée de l'oreille interne et la cuiller, instrument servant à manger les escargots).

 

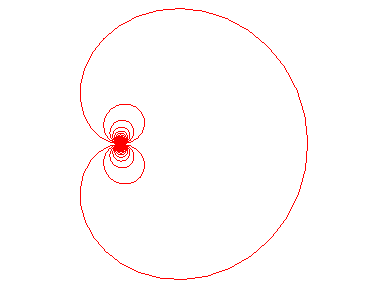
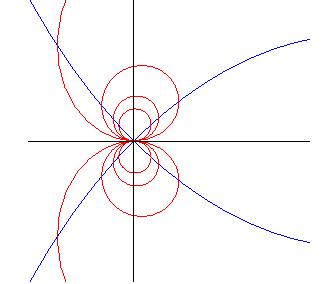
Équation polaire :  . Paramétrisation cartésienne : . Équation cartésienne : . Angle tangentiel polaire : . Courbe transcendante.

 
 

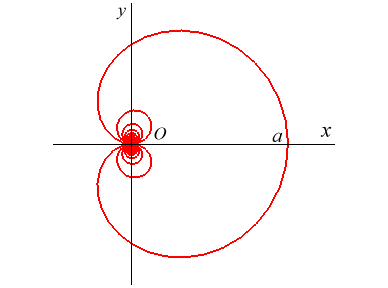La cochléoïde est le lieu de l'extrémité d'un arc de cercle de longueur fixe a dont l'autre extrémité est fixe et tangente à une droite fixe. On peut concrètement imaginer la courbe décrite par l'extrémité d'un tuyau en plastique prenant une forme circulaire, dont l'autre extrémité est fixée.	L'arc de cercle en gras reste de longueur constante
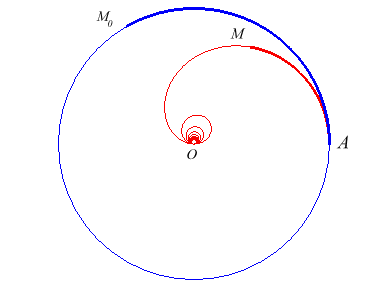
La cochléoïde est aussi la barycentrique du cercle ; plus précisément, c’est le lieu du centre de gravité M d'un fil pesant homogène enroulé autour du cercle de centre O et de rayon a (l'une des extrémités située en A de coordonnées polaires (a, 0) et l'autre en ) .	Le point M est centre de gravité de l'arc AM0
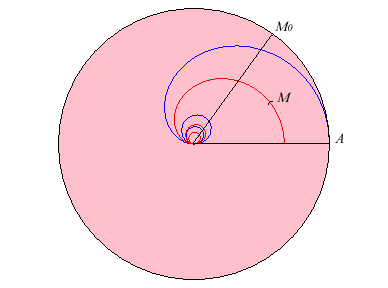
Le lieu du centre de gravité du secteur circulaire délimité par [OA] et [OM0] est aussi une cochléoïde, homothétique dans le rapport 2/3 : .
La cochléoïde est aussi l’inverse par rapport à O de puissance a2 de la quadratrice de Dinostrate : .
Si un point N décrit la spirale hyperbolique : , le point  décrit la cochléoïde. Autrement dit la cochléoïde est une partie de la strophoïdale de la spirale hyperbolique ; l'autre partie, décrite par  décrit une " syncochléoïde ", d'équation polaire .
La cochléoïde est la courbe limite des courbes de paramétrisation complexe : , donc d'équation polaire , le cas n = 4 donnant la néphroïde de Freeth.

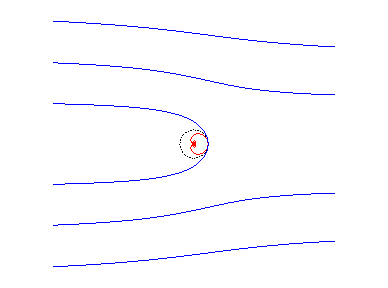
La cochléoïde est l’une des perspectives coniques d’une hélice circulaire, le centre de perspective étant un point de l’hélice et le plan de projection perpendiculaire à son axe ; par conséquent, la partie inférieure de la cochléoïde représente la vision en perspective d’une hélice tracée sur un tube cylindrique, quand l’oeil est au niveau du plafond.
 

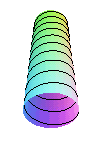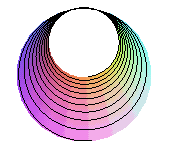
oeil au plafond du tube : on obtient  la cochléoide

oeil au centre : on obtient la spirale hyperbolique

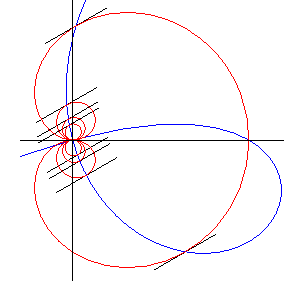
Les points de contact des tangentes à la cochléoïde faisant un angle  avec (Ox) se trouvent sur la strophoïde :  qui est droite lorsque  et se réduit à un cercle pour .
 

les points à tangente horizontales sont sur un cercle

les points à tangente verticale sont sur une strophoïde droite

les points à tangente de direction donnée oblique sont sur une strophoïde oblique.

 

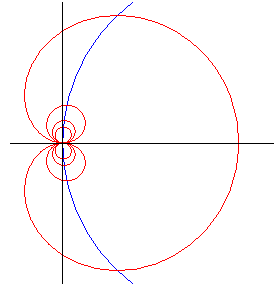courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2020