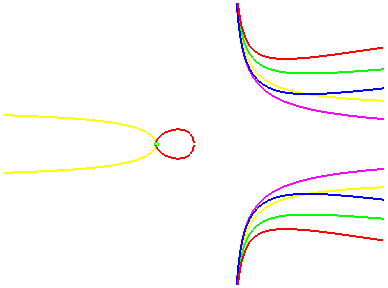
vert : cubique acnodale
bleu : cubique elliptique à une branche
jaune : cubique crunodale
magenta : cubique cuspidale
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
HYPERBOLE CUBIQUE
Cubical hyperbola, Kubische Hyperbel
|
|
rouge : cubique elliptique à ovale
vert : cubique acnodale
bleu : cubique elliptique à une branche
jaune : cubique crunodale
magenta : cubique cuspidale |
| Courbe étudiée par Newton en 1701.
Autres noms : hyperbole ambigène (nom donné par Newton), semi-trident, . |
Équation cartésienne : 
où P est un polynôme de degré inférieur
ou égal à 3 de
valuation nulle. Cubique. |
La transformation homographique : 
ramène cette cubique à la parabole
divergente droite
.
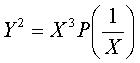
Comme les paraboles
divergentes (ainsi que les cubiques
de Chasles), les hyperboles cubiques représentent donc les perspectives
de toutes les cubiques.
La cubique d'Agnesi et la cubique de Lamé en sont des cas particuliers.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL, Jacques MANDONNET 2001