Courbe étudiée par Fritz Hügelschäffer en 1948, Maja Petrovic en 2011.

 

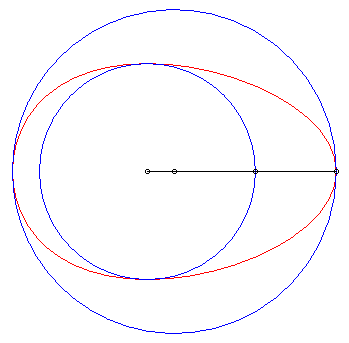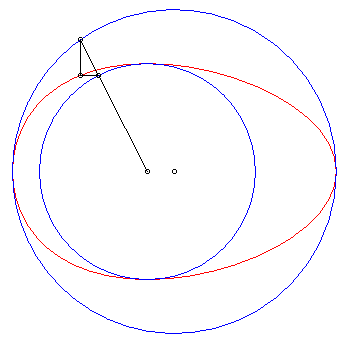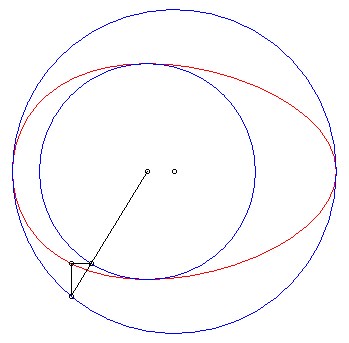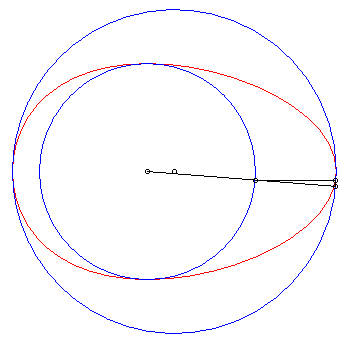
L'oeuf de Hügelschäffer est la transformée de Newton de 2 cercles par rapport à un repère Oxy , O étant le centre du premier cercle et le deuxième étant centré sur Ox. Lorsque les deux cercles sont concentriques, on obtient la construction classique de l'ellipse par réduction d'ordonnée ; le fait de décaler l'un des cercles désymétrise l'ellipse et donne, lorsque le cercle de centre O est inclus dans l'autre, une courbe en forme d'oeuf. Paramètres pour la courbe ci-contre : a = 6, b = 4, d = 1.

 

Équation cartésienne pour un cercle de centre O de rayon b et le deuxième cercle de centre (d, 0) et de rayon a :  ou . Cubique elliptique à ovale (sauf cas particuliers). Paramétrisation cartésienne : . Aire de l'ovale : . Volume de l'ovoïde obtenu par rotation autour de l'axe : .

 

Comme toute cubique, la courbe algébrique complète ne comporte pas que la forme ovoïde mais aussi une branche allant à l'infini. La deuxième équation ci-dessus montre d'ailleurs que les œufs de Hügelschäffer sont en fait équivalents aux hyperboles cubiques d'équation  avec P de degré 2 (P pouvant avoir le degré 3 pour une hyperbole cubique quelconque).

 

L'autre transformée de Newton (obtenue en échangeant les axes) possède aussi des allures d'œufs pour certaines valeurs du paramètre (ci-contre, en vert, pour a = 4, b = 6, d  = 1). Bizarrement ce n'est plus une portion de cubique mais une demi-sextique (l'autre moitié étant sa symétrique par rapport à Oy). La courbe verte ci-contre n'est pas la symétrique de la courbe rouge ci-dessus ! Équation de cette sextique : .

 

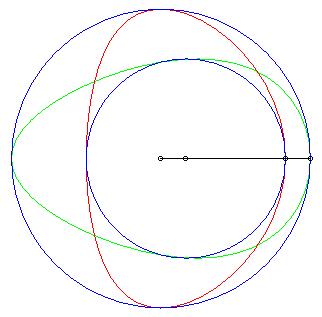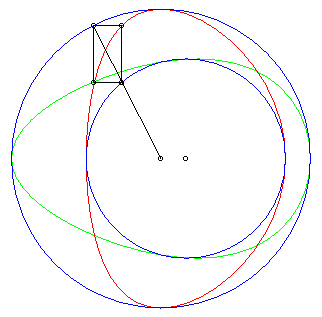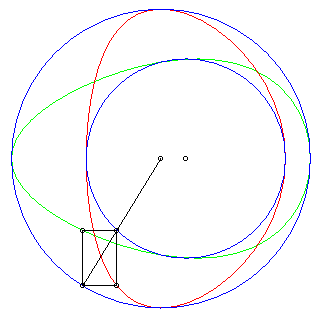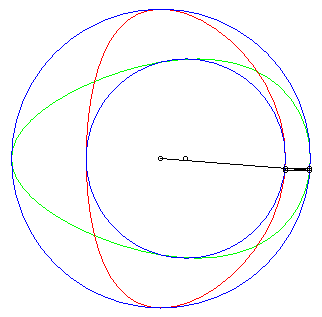Lorsque le deuxième cercle est centré sur le premier (d = a), la première transformée de Newton se décompose en une parabole et une droite, et la deuxième se décompose en une lemniscate de Gérono et une droite double.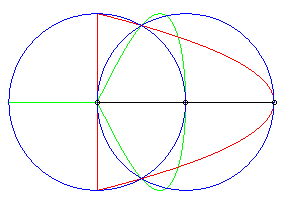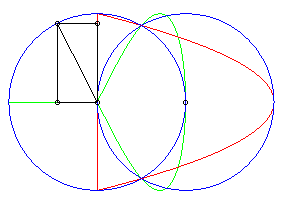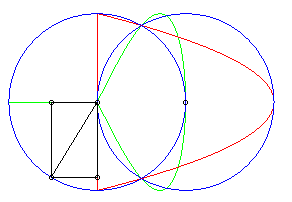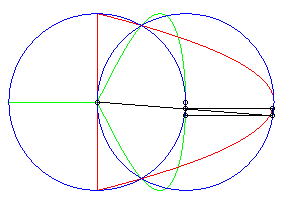
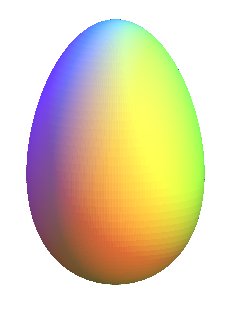
Vue de la surface obtenue par rotation autour de l'axe.

Voir aussi l'œuf d'Ehrart, et ce répertoire des courbes en forme d'œuf.

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2022