Curve studied by Fritz Hügelschäffer in 1948.

 

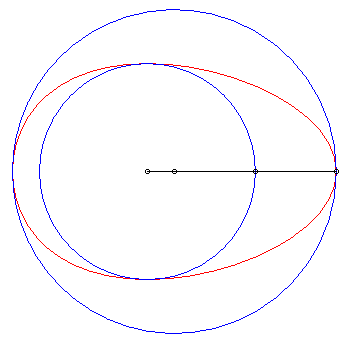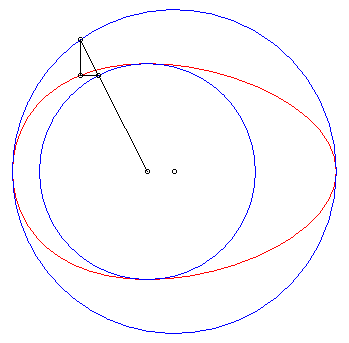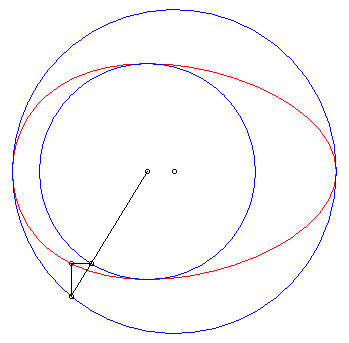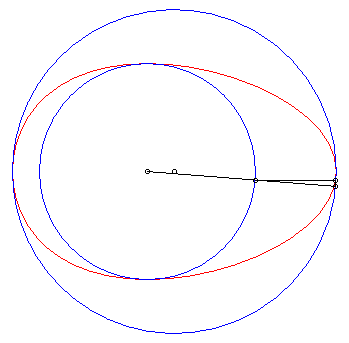
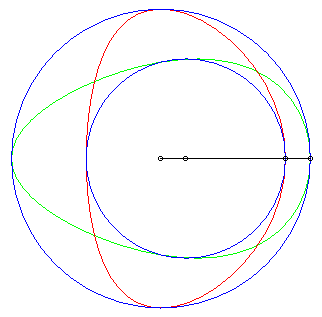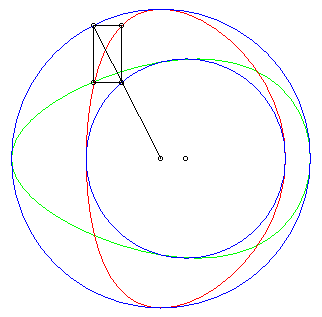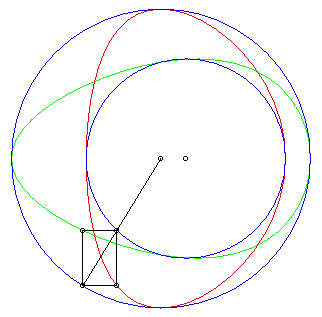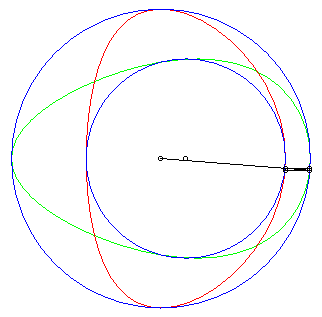
The Hügelschäffer egg is the Newton transform of 2 circles with respect to the frame Oxy, O being the centre of the first circle and the second one being centred on Ox. When the two circles are concentric circles, we get the classic construction of the ellipse by reduction of the ordinates; moving one of the circles makes the ellipse no longer symmetrical and gives, when the circle with centre O is included in the other one, a curve shaped like an egg. Parameters for the curve opposite: a = 6, b = 4, d = 1.

 

Cartesian equation for a circle with centre O and radius b and a circle with centre (d, 0) and radius a:  or . Elliptic cubic with an oval (except special cases). Cartesian parametrization: .

 

Like all cubics, the complete algebraic curve does not only include the ovoidal shape but also has an infinite branch. Besides, the second equation above shows that the Hügelschäffer eggs are in fact equivalent to cubic hyperbolas with equation  where P is a polynomial of degree 2 (P can be of degree 3 for other cubic hyperbolas).

 

The other Newton transform (obtained by swapping the axes) also has the shape of eggs for certain values of the parameter (opposite, in green, for a = 4, b = 6, d  = 1). Strangely, it is no longer a portion of a cubic but a half-sextic (the other half being its symmetric image about Oy). The green curve opposite is not the symmetric image of the red curve above! Equation of this sextic: .

 

When the second circle is centred on the first one (d = a), the first Newton transform is composed of a parabola and a line, and the second one is composed of a lemniscate of Gerono and a double line.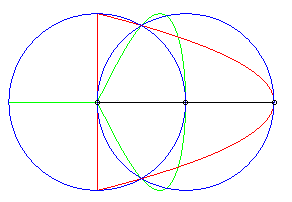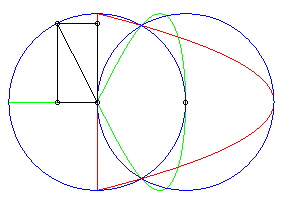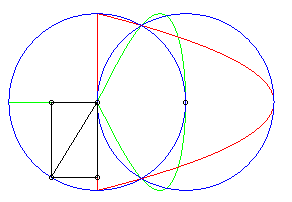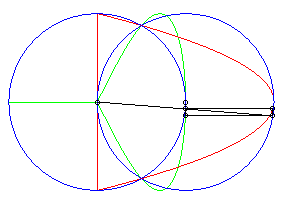

See also the Ehrart egg, and this index of the curves shaped like eggs.

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017