Polar equation: 
Opposite, n = 3 and 4.
See other trefoils at the bottom of the page dedicated to the quadrifolium.
............................
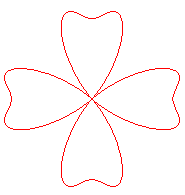
(Eugen Beutel: Algebraische Kurven, G.J. Göschen, Leipzig 1909-11)
Cartesian equation:
Non-rational sextic.
....................
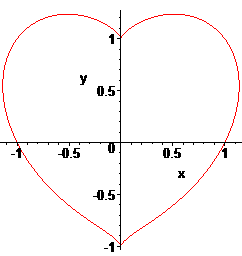Curve discovered by the author at the age of 16 for his
girlfriend...
Cartesian parametrization: 
Rational biquartic.
Cartesian equation:
x^8-x^6+27*x^4-27*x^2+12*y*x^6-12*y*x^4+42*y^2*x^4
+42*y^2*x^2+2*y^3*x^4+26*y^3*x^2+8*y^3+12*y^4*x^2+12*y^4+6*y^5+y^6=0
.......
Polar equation:
(portion of a curve that can in fact be extended on both sides of the sharp point)
i.e. 
This heart is composed of one half of the reunion of two eight-like quartics:
and 
.
Therefore, two eights = two hearts!
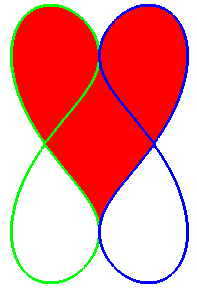
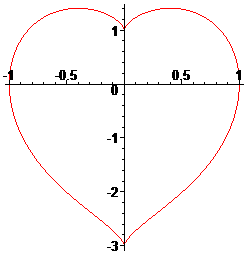
Cartesian equation (non-rational biquartic):
-108-36*y^2-448*x^2*y+112*x^2*y^2+405*x^4-112*y^3+12*y^4+66*x^4*y^2+224*x^4*y+128*x^2*y^3+24*y^4*x^2+
30*x^6+24*y^5+4*y^6+x^8-328*x^2+216*y+8*x^6*y+2*x^6*y^2+8*x^4*y^3+y^4*x^4=0
For an index of heart-like curves:
www.mathematische-basteleien.de/heart.htm
mathworld.wolfram.com/HeartCurve.html
See conchoid of a circle.
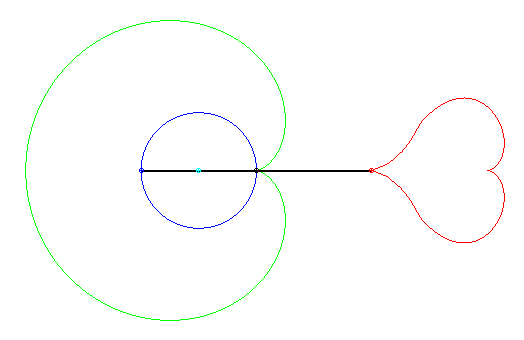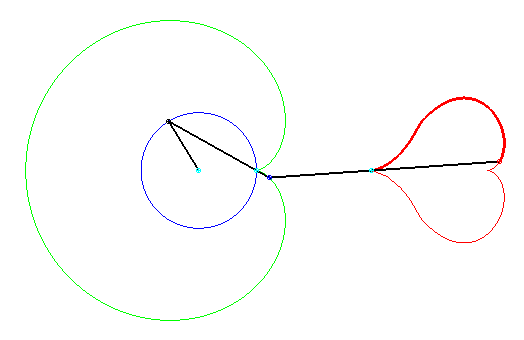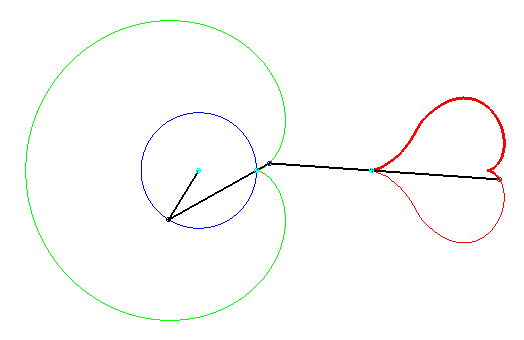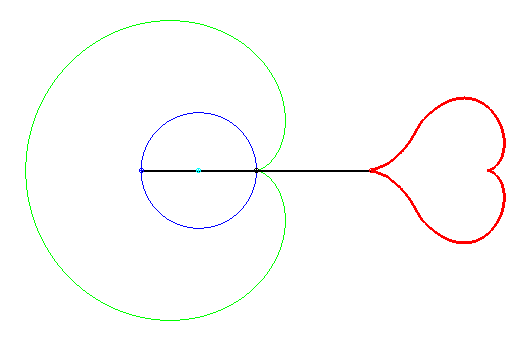
Punctual equation: 
I do not know the original parameters chosen by Ehrahrt
(who said that with these parameters, the curve coincides, up to the thickness
of the pencil stroke, with the shape of an egg obtained by a statistical
study).
Here, A = (0 ; 0), B = (0 ; 0,2), C = (0 ; 1), cte = 2,2.
Ehrhart called these curves "hyperellipses with 3 foci"; they are referred to on this site as triellipses.
See other eggs at ovoid.
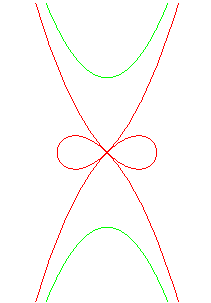
Polar equation: 
.
Cartesian equation: 
or 
Asymptotic parabolas (in green): 
.
Variation: 
,
i.e. 
,
the eight-like portion being the lemniscate
of Gerono.
Cartesian equation : 
.
Polar equation : 
.
Polar equation:
(on the right
).
L. Sautereau butterflies (2010 ?)
See also the Cundy and Rollett butterfly.
Polar equation:
Cartesian equation:
On the right: 
Closer:
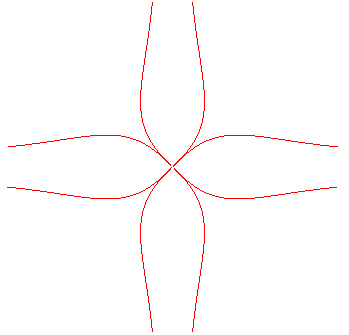
Polar equation:
for 
(opposite
with a = p/2), plus the circle 
.
Variation with the asymptotic circle on the right:
,
i.e. 
,
with a = 1/2.
Take two curves like
,
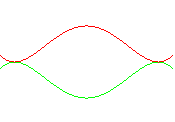for example 
and rotate around the symmetry axis.
See also here.
