Polar equation:  with n a positive real number. Algebraic curve iif n is rational. Area for e < 1 and n integer: . Special case where the curvilinear abscissa can be easily integrated: , or  (hence when e > 1, n <1): Curvilinear abscissa in this case : .

The cyclic-harmonic curves are the conchoids of roses with respect to their centre.
They also are the images by the Brocard transformation of Pascal limaçons, with respect to their pole.
The curve is composed of a base pattern, symmetrical about Ox, obtained for :
 

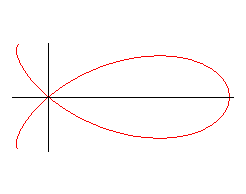
base pattern when e > 1

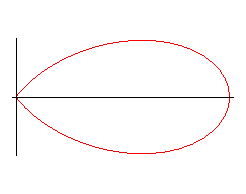
base pattern when e = 1

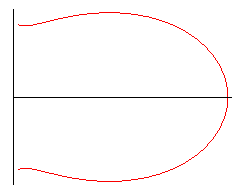
base pattern when e < 1

transformed by all the rotations of  for integer values of k.
When n is a rational number and p is its numerator, p rotations give the whole curve.

Case e < 1:
For n = p / q, the cyclic-harmonic curve of parameter n is one of the possible projections of the Turk's head knot of type (p,q); its p external summits and its p internal vertices form a regular polygon, and it has p(q-1) double points.
 

n = 1	n  = 2: peanut	n = 3	n = 4	n = 5: starfish
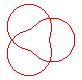
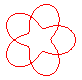
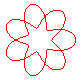
n = 1/2	n = 3/2 projection of the trefoil knot	n = 5/2 projection of the 5.1 knot	n = 7/2	n = 9/2
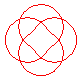
n  = 1/3	n = 2/3 projection of the figure-eight knot	n = 4/3 projection of the 8.18 knot	n = 5/3 projection of the 10.123 knot	n = 7/3
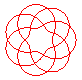
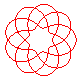
n = 1/4	n = 3/4 projection of the 9.40 knot	n = 5/4	n = 7/4	n = 9/4
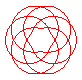
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5

Case e = 1:

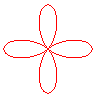
n = 1: cardioid	n  = 2: double egg	n = 3	n = 4	n = 5
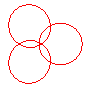
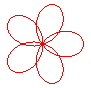
n = 1/2	n = 3/2	n = 5/2	n = 7/2	n = 9/2
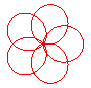
n  = 1/3	n = 2/3	n = 4/3	n = 5/3	n = 7/3
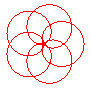
n = 1/4	n = 3/4	n = 5/4	n = 7/4	n = 9/4
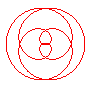
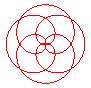
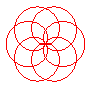
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5

Case e > 1, Trojan roses:
 

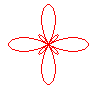
n = 1: limaçon of Pascal with a loop	n  = 2: trisectrix of Ceva	n = 3	n = 4	n = 5
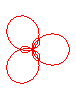
n = 1/2: Freeth's nephroid	n = 3/2	n = 5/2	n = 7/2	n = 9/2
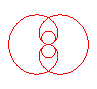
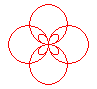
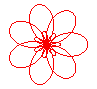
n  = 1/3	n = 2/3	n = 4/3	n = 5/3	n = 7/3
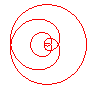
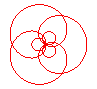
n = 1/4	n = 3/4	n = 5/4	n = 7/4	n = 9/4
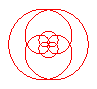
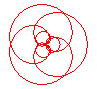
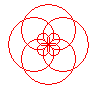
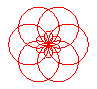
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5

The cyclic-harmonic curves the toroidal solenoids viewed from above.

The inverses of cyclic-harmonic curves are the polygasteroids.

Also compare with the folioids.
 

Remark: if we put an absolute value around the cosine, the starfish becomes a sunflower:

The students of classes préparatoires did not miss the shape of the cyclic-harmonic curve when n = 3 and e < 1: , with a slight dilatation, and called it cockoid:  On the right, a more elaborated version: .

 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017