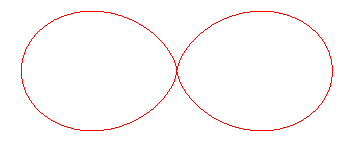
DOUBLE EGG CURVE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
DOUBLE EGG CURVE

| Curve studied by Villalpando in 1606 and by Münger
in 1894.
Other names: bioval, proportionatrix curve (name given by Villalpando). |
| Polar equation: Cartesian equation: Curvilinear abscissa: Radius of curvature: Length of an egg: Area of an egg: Rational sextic. |

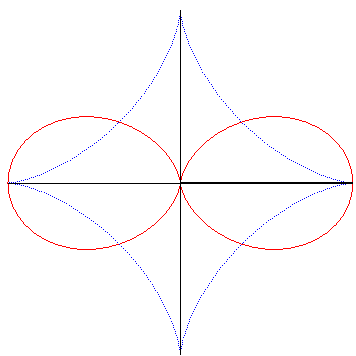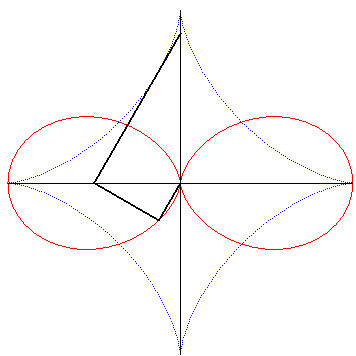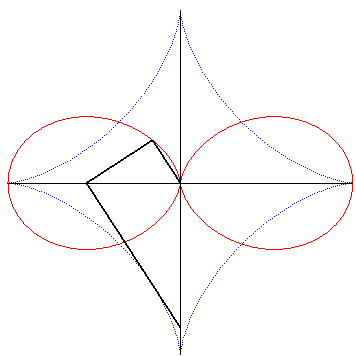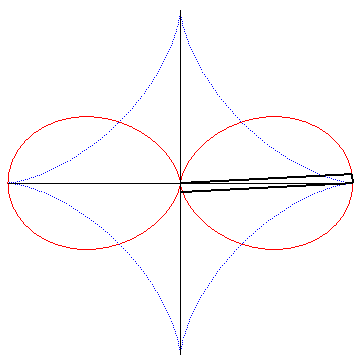
Double egg and its evolute; the curvature is infinite at the centre. |
The double egg curve is the Clairaut
curve with the above polar equation, which shows that it is a conchoid
of the quatrefoil.
| It is also the inverse of the Kampyle of Eudoxus with respect to its centre: |  |
| And it is obtained by the following construction: given a segment line of constant length constrained to have its ends moving on two perpendicular lines intersecting at O, the projection of O on a line perpendicular to the segment at one of its ends describes the double egg. |
 |
| The double egg is the glissette of the tip of a cardioid constrained to stay tangent to a fixed line at a fixed point. |
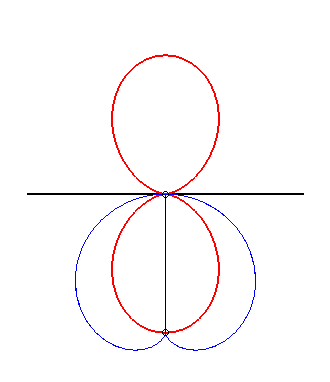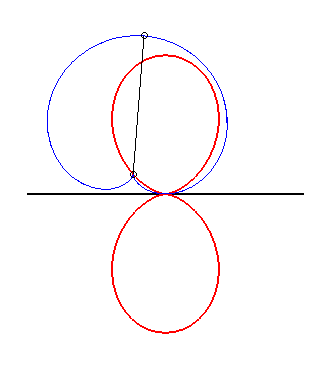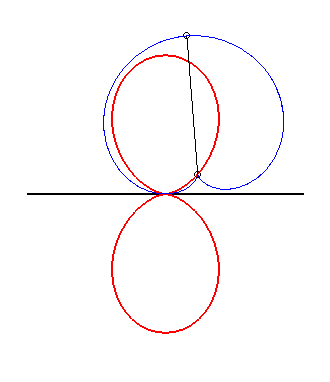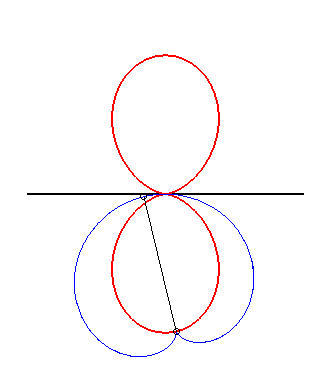 |
| It can also be obtained by an ellipse rolling on a quadrifolium. |
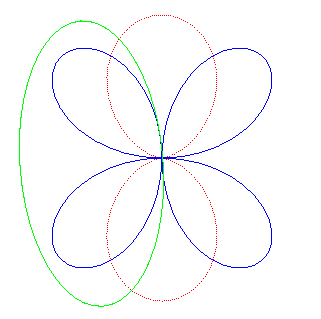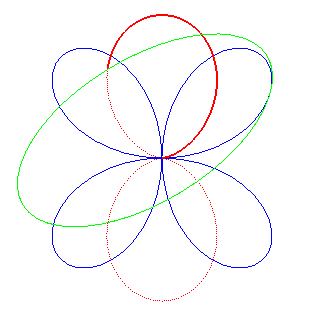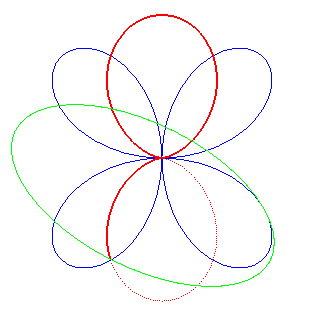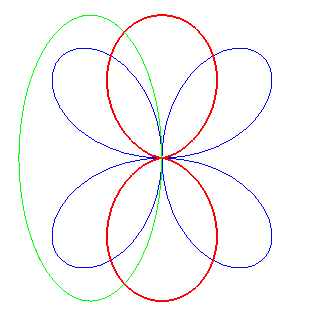 |
| The magnetic
field lines created by a magnetic dipole are double eggs; the orthogonal
lines are the curves with polar equations |
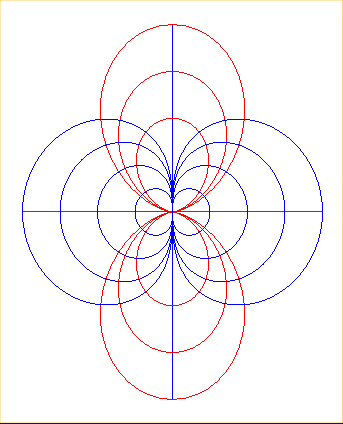 |
| The road associated to the wheel shaped like a double egg so that the centre has a linear motion is the image of a cycloid by a 1/2 scaling in one direction (animation by Alain Esculier) | 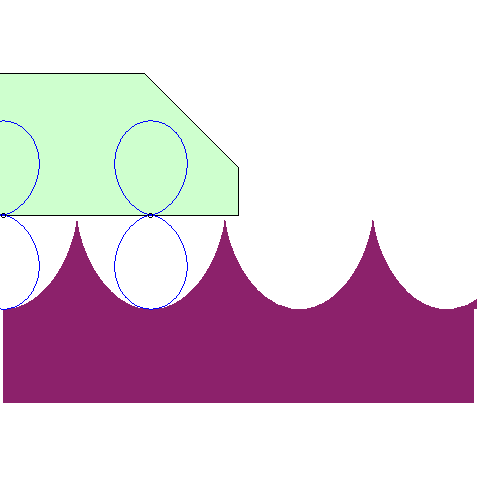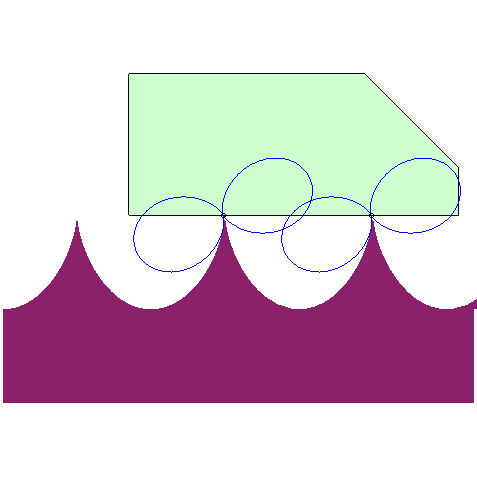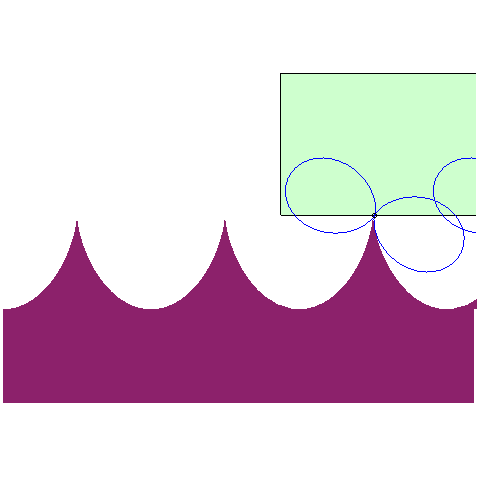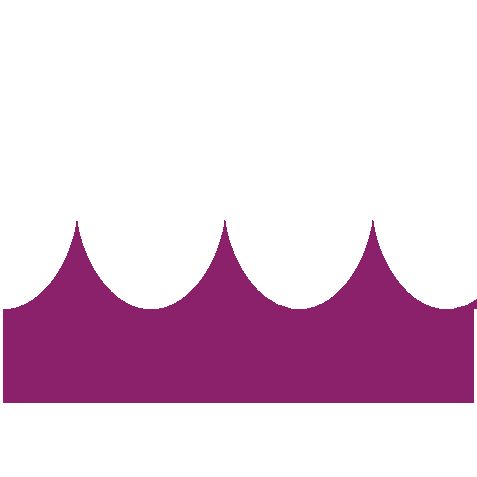 |
Compare to the simple
folium (
instead of
)
and look at other eggs at ovoid.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017