Multifocal ellipse

MULTIFOCAL ELLIPSE or EGGLIPSE

Curve studied by Tschirnhaus in 1686, and Maxwell in 1846.
Other names: multiellipse, polyellipse, hyperellipse, Tschirnhaus egg.
Sites :
English Wikipedia (N-ellipses)
English Wikipedia (Generalized conic)
French Wikipedia (point de Fermat-Weber)
http://www.aimath.org/WWN/convexalggeom/AIM.pdf
On the Approximation of Convex, Closed Plane Curves by Multifocal Ellipses
text by Maxwell
article on the algebraic side
on the triellipses
http://www.journaloftheoretics.com/Articles/6-6/MFCC.pdf?q=foci
on the Fermat point
Gyula Sz.-Nagy (June 1950). "Tschirnhaus'sche Eiflachen und EiKurven". Acta Mathematica Academiae Scientiarum Hungarica 1 (2): 167–181.

The multifocal ellipses, with n foci, are the loci of the points of the plane for which the sum of the distances to n points is constant.
Multipolar equation: .
The case n = 1 gives, of course, the circles.
The case n = 2 gives the classic ellipses. More precisely, is, at the minimum, AB and when , gives the ellipse with foci A and B and major axis a, reduced to the segment line [AB] when a =AB.

For n = 3, the minimal value of is reached at a unique point F, called the Fermat point of the triangle ABC, and the ellipses with three foci, called triellipses, form concentric ovals around F.
If the angles of the triangle are acute, then the Fermat point is defined by the fact that, from it, the sides are seen under 120° angles (example opposite).
If one of the angles is greater than or equal to 120°, then the Fermat point is the corresponding vertex; in the flat case with distinct vertices, the Fermat point is the middle vertex. If two points coincide, they also coincide with the Fermat point, and we get a Cartesian oval.
The minimal value of the sum is where , and a,b,c are the sides of the triangle.
As we can see opposite, the triellipses have a tangent at all point except when they pass by the vertices of the triangle.

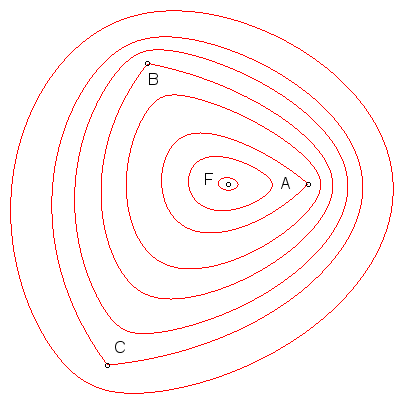Generalisation of the gardener's ellipse-tracing method for a triellipse, proposed by Maxwell.

Opposite, the case of an equilateral triangle.

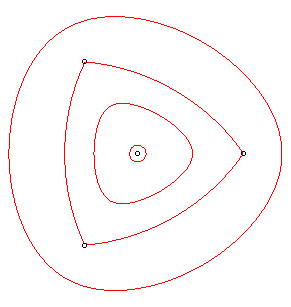Since the product of the eight terms is a polynomial function of , the curve with equation = 0 (called Helton-Vinnikov curve) is algebraic of degree 8, and contains the triellipse .
For example, the equation of the algebraic curve corresponding to the triellipse passing by the vertices of the previous equilateral triangle, represented opposite, is:
1331+2628*x^2*y^2+1314*x^4+1314*y^4+512*x^3-124*x^6-372*x^2*y^4-124*y^6+12*x^2*y^6+
12*x^6*y^2+3*y^8+3*x^8-1536*x*y^2-372*x^4*y^2+18*x^4*y^4-3036*x^2-3036*y^2=0
The triellipse is only composed of the central red triangle; the three blue, green and yellow curves correspond to the equations with two "+" signs (the four others do not have real points).
In the other cases, the triellipse is only an oval connected component of the algebraic curve, that can contain at most four of them.

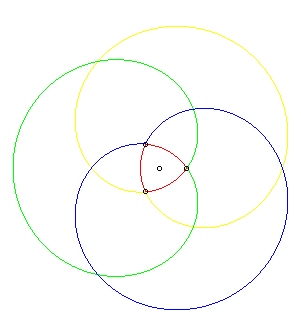As for the ellipse, the tangent to the ellipse is constructed perpendicularly to the vector .

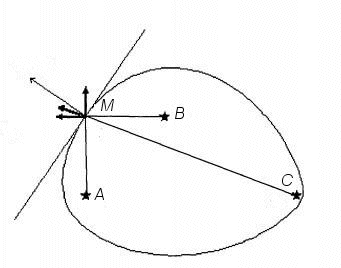For , the minimal sum is always obtained at a unique point, called the Fermat-Weber point.
The n-ellipse is included in an algebraic curve of degree , that can be lowered to when n is even.
Opposite, the quadriellipse passing by the vertices of a square, and the associated algebraic curve, of degree 16 – 6 = 10.

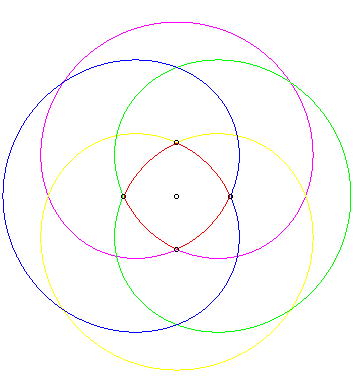Compare to the Cassinian curves, with equation .

Animation of the complete triellipse associated to an equilateral triangle, starting from a = 0.
For large values of a, the curve tends to become a circle centred on the barycentre of .

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

For n = 3, the minimal value of is reached at a unique point F, called the Fermat point of the triangle ABC, and the ellipses with three foci, called triellipses, form concentric ovals around F. If the angles of the triangle are acute, then the Fermat point is defined by the fact that, from it, the sides are seen under 120° angles (example opposite). If one of the angles is greater than or equal to 120°, then the Fermat point is the corresponding vertex; in the flat case with distinct vertices, the Fermat point is the middle vertex. If two points coincide, they also coincide with the Fermat point, and we get a Cartesian oval. The minimal value of the sum is where , and a,b,c are the sides of the triangle. As we can see opposite, the triellipses have a tangent at all point except when they pass by the vertices of the triangle.
Generalisation of the gardener's ellipse-tracing method for a triellipse, proposed by Maxwell.
Opposite, the case of an equilateral triangle.
Since the product of the eight terms is a polynomial function of , the curve with equation = 0 (called Helton-Vinnikov curve) is algebraic of degree 8, and contains the triellipse . For example, the equation of the algebraic curve corresponding to the triellipse passing by the vertices of the previous equilateral triangle, represented opposite, is: 1331+2628x^2y^2+1314x^4+1314y^4+512x^3-124x^6-372x^2y^4-124y^6+12x^2y^6+ 12x^6y^2+3y^8+3x^8-1536xy^2-372x^4y^2+18x^4y^4-3036x^2-3036*y^2=0 The triellipse is only composed of the central red triangle; the three blue, green and yellow curves correspond to the equations with two "+" signs (the four others do not have real points). In the other cases, the triellipse is only an oval connected component of the algebraic curve, that can contain at most four of them.
As for the ellipse, the tangent to the ellipse is constructed perpendicularly to the vector .
For , the minimal sum is always obtained at a unique point, called the Fermat-Weber point. The n-ellipse is included in an algebraic curve of degree , that can be lowered to when n is even. Opposite, the quadriellipse passing by the vertices of a square, and the associated algebraic curve, of degree 16 – 6 = 10.