SWIMMING DOG CURVE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
SWIMMING DOG CURVE
| Curve studied by Saint Laurent and Sturm in 1822.
Homemade name. For the travel times, see www.feynmanlectures.caltech.edu/info/exercises/boat_time.html. |
The swimming dog curve is the trajectory of a dog
in a river, resisting to a linear current with speed 
by swimming at constant speed 
towards a fixed point on the bank (here, the fixed point is O and
the current flows in the direction Oy); one can also imagine a boat
going towards a fixed beacon.
Differential system giving the movement of the swimming
dog:
in Cartesian coordinates, i.e. 
in polar coordinates.
Differential equation of the trajectory:
|
Note that the swimming dog reaches the fixed point iff
the speed of the current is less than its speed; as the speed of the current
increases, the travel time increases too, until the case where 
;
the dog theoretically still reaches the bank Oy, but downstream
from the target, and in an infinite time; its trajectory is then an arc
of a parabola with focus O.
When the speed of the current is greater than its speed, it is carried
away by the stream.
 |
 |
 |
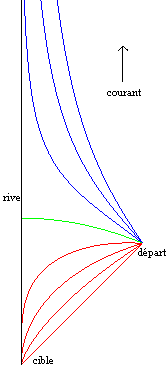| Above, three representations of the curves, depending
on whether the starting point of the dog is downstream, in front of, or
upstream from the target.
No current: case =
0: linear trajectory.
In red: case  ,
i.e. k > 1: the dog still reaches its target after a detour.
In green: case ,
i.e. k = 1: the dog still reaches the bank, but not the target (the
curve is a parabola)
In blue: case  ,
i.e. k < 1: the dog gets closer to the bank but never reaches
it. |
The trajectory of the dog in the moving plane linked to the river is a pursuit curve (which gives a method for solving this problem).
This problem can be generalised by considering two planes (P) and (Q), the first one being fixed while the second one moves, and the curves traced on (P) by a point M of (Q) moving constantly towards a fixed point O, at constant speed.
For example, if the movement of (Q) is a uniform circular motion with centre O, the curve of M in (P) is an Archimedean spiral.
Another generalisation consists in considering that the
axis of the dog (or rather the boat) forms a constant angle a
with (OM); we then get the polar differential equation: 
.
For k = 1, it is integrated into the parabola: 
.
For a = p/ 2,
the result is remarkable, since the movement is the same than that of the
planets around the Earth, see at conic.
We can also consider that the point in the direction of
which the dog is swimming is also moving, which gives a pursuit curve with
current.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017
in Cartesian coordinates, or 
in polar coordinates.
where 
with u = b/a.
.
