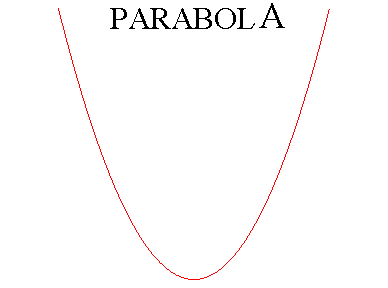
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |

| Curve studied by Menaechmus
in the 4th century BC, then by Archimedes, Apollonius, Pappus, Galileo
etc...
From the Greek parabolê "comparison, parabola", para "next to", and ballein "throw". |
 |
Reduced Cartesian equation: Polynomialconic. p (> 0): semi-latus rectum, or parameter, of the parabola. F(p/2, 0): focus of the parabola. (D), line with equation x = – p/2: directrix of the parabola. Reduced Cartesian parametrization: Polar equation: Curvilinear abscissa: Radius of curvature: Polar equation (pole F, axis Fx): |
The parabola is the conic with eccentricity 1.
It was historically defined as a section of the cone of revolution by a plane parallel to one of its generatrices:

The parabola has many planar geometrical definitions:
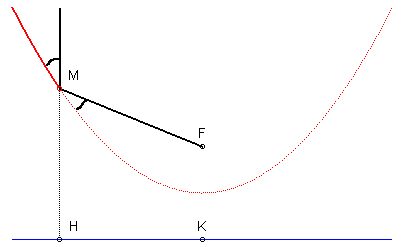
1) Definition by focus and directrix:
The parabola is the equidistance
curve between a point (the focus F) and a line (the directrix
(D)), in other words, the isotel
of a line, hence the construction:

MF = MH |
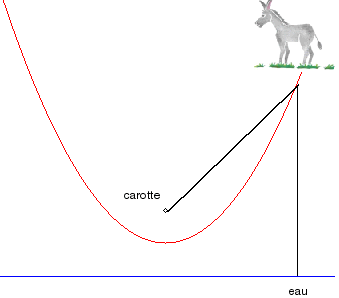
The parabola is the fatal indecision curve of the Buridan ass who has to chose between a carrot and water! |
| Therefore, the locus of the points M for which
the sum of the distances to a point F and a line D is a constant
equal to d is the reunion of two arcs of parabolas of focus F
and directrices located at distance d from D.
Hence the construction of an arc of a parabola by a method similar to the gardener's tracing method of an ellipse. |
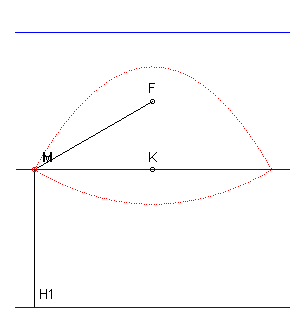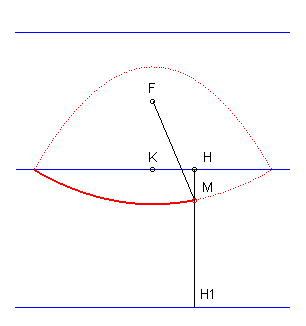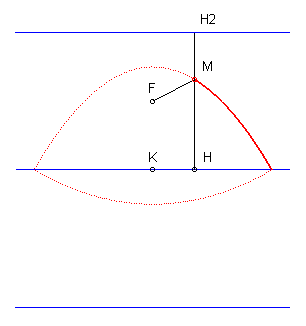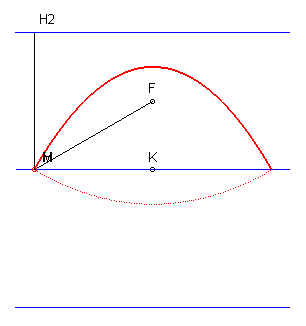 |

Figure taken from the "bible": Lebossé Hémery |
| More generally, the equidistance curves between a circle and a line are reunions of two parabolas: |
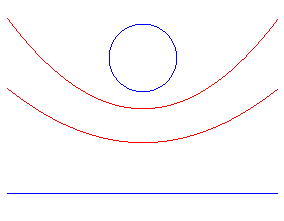
see here the corresponding sand pile. |
The construction of the focus and the directrix of the
parabola defined as a section of a cone is given by the Dandelin theorem
and illustrated below:
 |
The tangency point of the sphere inscribed in the cone and tangent to the plane of the parabola is located at the focus of the parabola, and the intersection between the plane of the contact circle and the plane of the parabola is the directrix. |
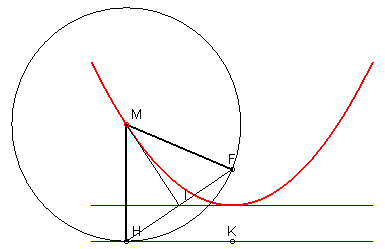
Moreover, the tangent at M is the interior bisector of the angle FMH:
Applications:
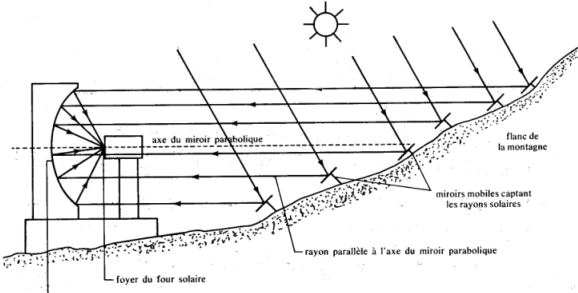
|

To shoot the ball into the hole, shoot it parallel to the side! |
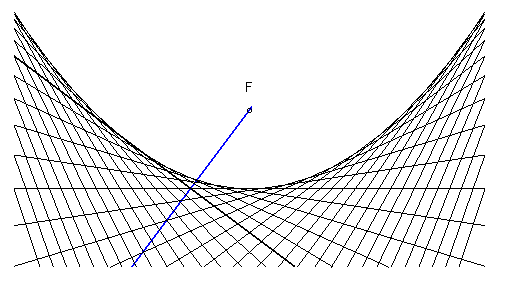
2) Definition as the negative pedal of a line.
The parabola is the envelope of the perpendicular at
I
to the line (FI), when I describes the tangent at the vertex
of the parabola (x = 0) (in other words, the parabola is the negative
pedal of this line with respect to the focus); thus, it is also the
envelope of the mediatrix of the segment line [FH], when H
describes the directrix (in other words, the orthotomic
of the parabola with respect to its focus is the directrix).
 |
Application 1: construction method using a set-square. |
 |
3) The parabola is the envelope of a line passing by two
points in linear uniform motions (see also Lamé
curve).
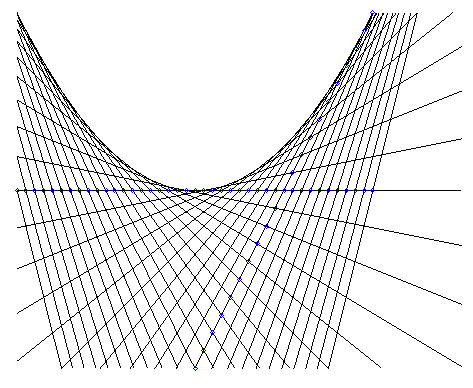 |
 The curves obtained in a wire table with linear vertical edges are therefore arcs of parabolas, and not arcs of circle as could be hastily thought. |
4) The parabola is an anticaustic of a line.
5) The parabola is a Ribaucour curve.
6) The parabola is the curve with constant sub-normal
() or the curve
with sub-tangent equal to twice
the abscissa (
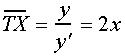
The pedals of parabolas are the rational circular cubics (see pedal).
The evolute
of the parabola
is the semicubical
parabola;
.
Note that all the parabolas are similar to one another, and that the image of a parabola by any affine transformation is a parabola, and therefore is similar to the initial parabola.
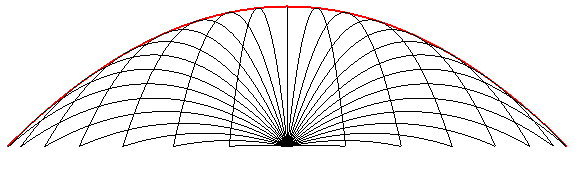
The trajectories of a massive point in a constant gravitational
field are lines or parabolas:
|
|
 |
and, similarly, the streamlines of an tilted plane are lines or parabolas.

 |
Equation of a shot: Equation of the safety parabola: with The shooting point is at the focus of the safety parabola. |
See also what happens to this with a fluid
friction as well as this beautiful
problem.
| We also get a parabola when a liquid constrained between
two slabs of glass is in rotation; the parameter of the parabola is equal
to |

example with g = 10 and omega = 5 radians per second |
| The theoretical curve of the upper cable of a suspension bridge can be considered to be a parabola, as opposed to that of a free hanging wire, that assumes the shape of a catenary. |  |
| Ditto for the arch of a viaduct like the one in Garabit: |  |
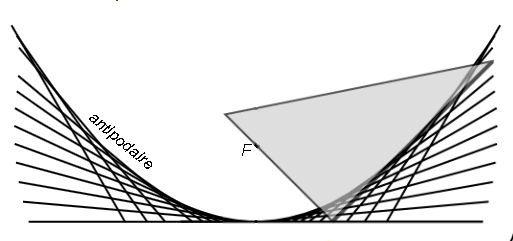
See the curves parallel to the parabola here.
See also the curve of
the swimming dog and the paraboloids.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017