Archimedean spiral

ARCHIMEDEAN SPIRAL

Discovery of the curve attributed to Conon of Samos, disciple of Archimedes; modern study by Sacchi in 1854.
Archimedes of Syracuse (287-212 av. J.C.): Greek savant.
Other names: equilateral spiral, neoid.
Link to an animation of the compressor with spiral.

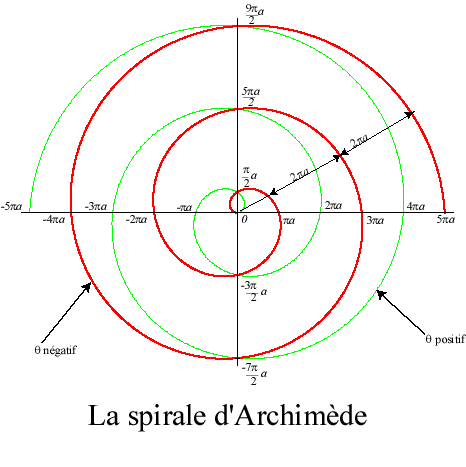	For a spiral with path : Polar equation: . Transcendental curve. Caracterisation: ( = tangential polar angle). Arc length: . Radius of curvature: . Length of the n-th spire obtained for : where is the mean of the lengths of the circles of radius ne and (n +1)e. Area sweeped by the radius vector for : , so that .
	For example, , that Archimedes already knew: "The surface of the first round of the spiral is equal to one third of the surface of the circle of which the radius is the length traveled by the point on the straight line during the first round".

The Archimedean spiral is the trajectory of a point moving uniformly on a straight line of a plane, this line turning itself uniformly around one of its points (carried out for example by the groove of a good old vinyl disk); here, O is the center of rotation, r = 0 for q = 0.

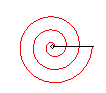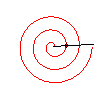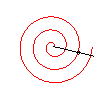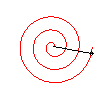
Now, notice the difference with the logarithmic spiral.

For example, a person on a turntable rotating at a constant speed and traveling at a constant speed towards the center, describes, in the fixed reference frame, an Archimedean spiral (see the curve of the swimmer and see also the circle involute for the case where the person does not go towards the center).

Once it is not customary, the complete spiral , which has double points, is clearly less aesthetic than the curve ... ...that does not, and shares the plan in two
connected, symmetric with respect to O, regions (cf. the spiral of Fermat). This is how this string was coiled.

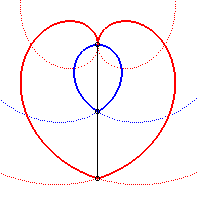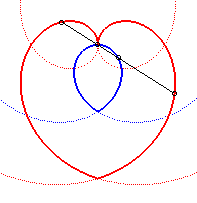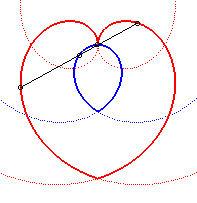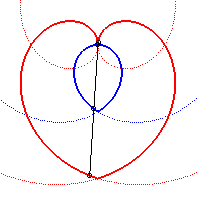
Remark: any conchoid of this spiral, of equation , is still an Archimedean spiral, that is an image of the previous one by a rotation of angle –b/a. This translates kinematicly into the fact that if an Archimedean spiral rotates around its center with a uniform movement, the intersection of the spiral with a line crossing by the center describe a uniform movement (this is used to transform a circular movement into a rectilinear movement, for example for the regular filling of a bobbin - cf. the former sewing machines; see also at circle involute).

Heart-shaped cam, formed of two branches of Archimedean spirals: the rotation movement is transformed into the succession of two straight rectilinear movements of opposite directions.

On the right of the sewing machine is the heart-shaped cam.

Other application: if a stick of length 2a is forced to slide at the top of an Archimedean spiral, and its middle is forced to pass through the central loop of this spiral, the ends describe the previous heart-shaped cam.

Chasles' Theorem: the Archimedean spiral is the roulette obtained by rolling a line on a circle with center O and radius a and taking a tracer point located at a distance to that line equal to the radius of the circle. The projected point of this tracer point on the line tracing a circle involute, we deduce that the Archimedean spiral is also the pedal curve of the circle involute.
This circle involute, which is therefore very simply constructed by rolling a straight line on a circle, is in fact a simple means of constructing the Archimedean spiral in an aproached fashion.

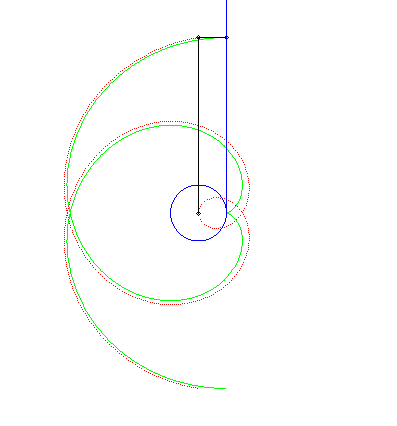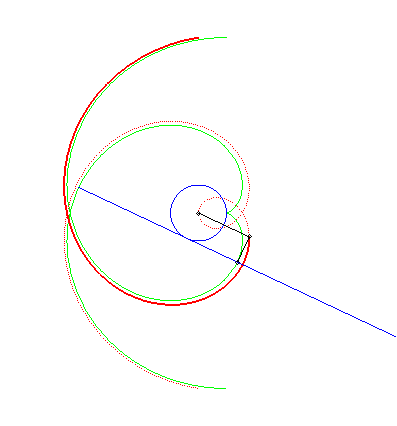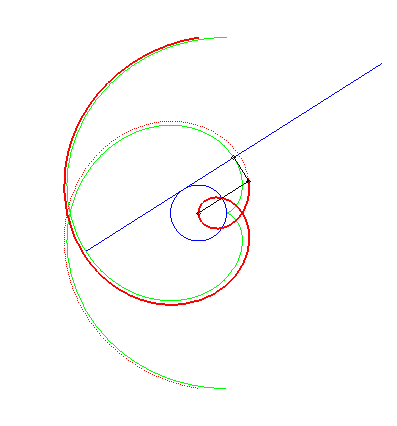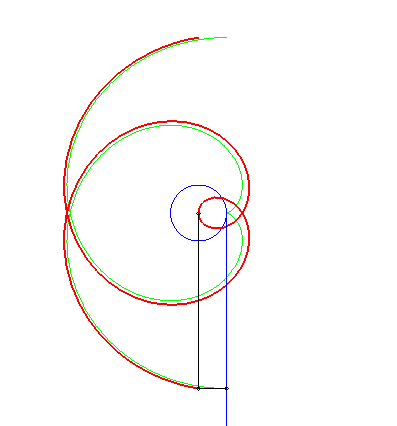As well as the golden spiral for the logarithmic spiral, the Archimedean spiral possesses approached constructions by arcs of a circle, as the spiral with 4 centers opposite (arcs of a circle are colored with the same color as the corresponding centers); this construction becomes widespread with any number of centers.

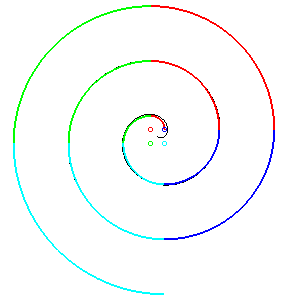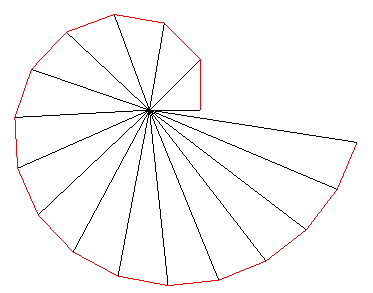
Problem: is the black Archimedean spiral (tangent in its center to the diagonal of the square) asymptotic to the spiral with 4 centers, as this figure suggest ?

The Theodorus (of Cyrene)'s said spiral, or snail of Pythagoras (in german, Quadratwurzelschnecke), provides an approached construction by right segments of an Archimedean spiral.
The construction of the 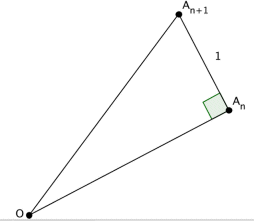vertices of the polygonal line is indicated below, starting from at a distance1 of O on Ox. The Pythagoras' theorem then shows that , hence the importance of this spiral.
has as polar angle and we show
that and that approaches a constant value = –2,15778......
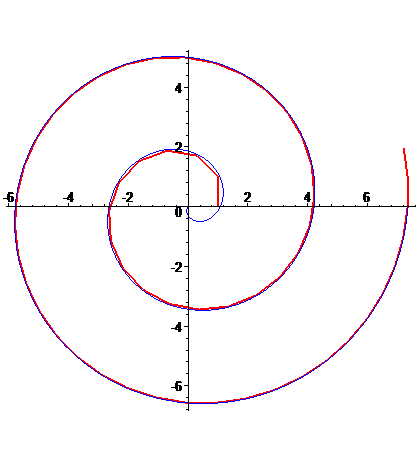The Theodorus spiral is then asymptotic to the Archimedean spiral as we well see on the figure to the right (in red, Theodorus, in blue, Archimedes).

The Archimedean spiral can also be defined as a curve with constant polar subnormal.

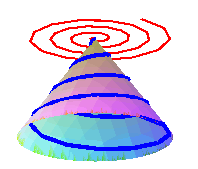
Finally, it is the (orthogonal) projection of the conic spiral of Pappus on a plane orthogonal to the axis of the cone.

The Archimedean spiral is:

- a quadratrix: if A is the point of polar angle and B the point of intersection of the tangent in A with Oy, OB / OA = .

- a trisectrix and even a n-sectrix : if a line of polar angle cuts it at , the circle with center O and a radius of cuts it in
.

See at wheel-road couple the rolling of an Archimedean spiral on a parabola.

See also the conical spiral of Pappus, the conical analogue of the Archimedean spiral, the clelie, its spherical analogue, the Doppler spiral, the constant angular acceleration curve.

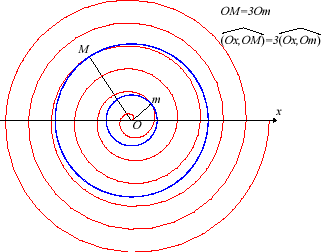
Any sequence of points of the complex plane whose modulus and amplitude are in arithmetical progression describes an Archimedean spiral.

For example, in the figure below, for n = 30, the points of polar coordinates have been plotted, in blue if l is even, in red otherwise; these points are staggered at the intersection of concentric circles of radii in arithmetic progression and concurrent lines; but they are also located on the Archimedean spirals of equation , hence a nice effect.

Spiral mosaics from Guy Barthélémy

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra


Once it is not customary, the complete spiral , which has double points, is clearly less aesthetic than the curve ...	...that does not, and shares the plan in two connected, symmetric with respect to O, regions (cf. the spiral of Fermat).	This is how this string was coiled.

Remark: any conchoid of this spiral, of equation , is still an Archimedean spiral, that is an image of the previous one by a rotation of angle –b/a. This translates kinematicly into the fact that if an Archimedean spiral rotates around its center with a uniform movement, the intersection of the spiral with a line crossing by the center describe a uniform movement (this is used to transform a circular movement into a rectilinear movement, for example for the regular filling of a bobbin - cf. the former sewing machines; see also at circle involute).
Heart-shaped cam, formed of two branches of Archimedean spirals: the rotation movement is transformed into the succession of two straight rectilinear movements of opposite directions.	On the right of the sewing machine is the heart-shaped cam.
Other application: if a stick of length 2a is forced to slide at the top of an Archimedean spiral, and its middle is forced to pass through the central loop of this spiral, the ends describe the previous heart-shaped cam.