.
The most famous case is the case n = 3, since it has no ruler-and-compass
construction; the corresponding curves are called trisectrices
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
SECTRIX CURVE
A sectrix is an auxiliary curve allowing to graphically
solve the problem of the section of an angle into n equal angles,
with n any integer .
The most famous case is the case n = 3, since it has no ruler-and-compass
construction; the corresponding curves are called trisectrices
Examples of families of n-sectrix curves:
- the Maclaurin
sectrices
- the Ceva
sectrices.
- the Delanges
sectrices.
Examples of n-sectrices for any n:
- the Archimedean
spiral
- the Dinostrate
quadratrix.
Examples de trisectrices:
- the conchoid
of Nicomedes
- the Maclaurin
trisectrix
- the Tschirnhausen
cubic (or Catalan trisectrix)
- the trisectrix
limaçon
- the rectangular
trefoil (or Longchamps trisectrix)
- the Ceva
trisectrix
- the Delanges
trisectrix
- the Dürer
folium
- the hyperbola
with eccentricity 2.
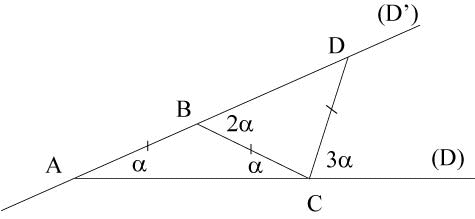
| Four of the nine previous trisectrices can be defined
from the opposite figure, attributed to Archimedes, enclosing an angle
and a triple angle.
In the two following constructions, the length L
is fixed.
If A and (D) are fixed, (D') rotates around A and C slides on (D), then the point D describes the Ceva trisectrix, with pole A (and the line (BC) envelopes an astroid). If C and D are fixed, (D) rotates around C and (D') rotates around D, then B can slide on (D') while describing a circle with centre C, but, most importantly, A describes the trisectrix limaçon, of pole D. In the 3 following constructions, the length L is variable. If A and C are fixed, and (D') rotates around A, then B describes the mediatrix of [AC], but most importantly, D describes the Maclaurin trisectrix, with pole A. If A and D are fixed, and (D) rotates around A, while B slides on (D'), then C describes a hyperbola with eccentricity 2. A fifth possibility, explored by Geneviève Tulloue,
is fixing D and (D), rotating (D') around D,
while A and C slide on (D). Then, the point B
describes the curve with polar equation |
AB = BC = CD=L |
Animation of the construction of the Ceva trisectrix by this method (animations realised with the Cabri software by Geneviève Tulloue)
Animation of the construction of the trisectrix limaçon by this method:
Animation of the construction of the Maclaurin trisectrix:
Animation of the construction of the hyperbola with eccentricity 2 by this method:
Animation of the construction of the Tulloue trisectrix by this method:
Link in Dutch about the trisectrices: www.pandd.demon.nl/trisect.htm#top
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017
,
that can be called "Tulloue trisectrix".