TSCHIRNHAUSEN CUBIC

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
TSCHIRNHAUSEN CUBIC

| Curve studied by Tschirnhaus in 1690, L'Hospital in 1696 and Catalan in 1832.
Name given in 1900 by R C Archibald, adding "en" at the end of Tschirnhaus' name. Other names: Catalan trisectrix, L'Hospital cubic, orthogenid [?loria]. Ehrenfried von Tschirnhaus (1651-1708): German geometrician and physicist. |
 |
In (O, Cartesian equation: Cartesian parametrization: Polynomial cubic with a double point. The summit is A(9a, 0) and the double point is O. Another partial Cartesian parametrization (in bold opposite): |
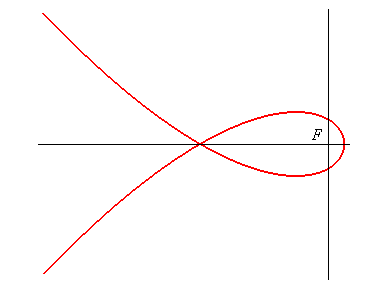 |
Cartesian equation in (F, Cartesian parametrization: Curvilinear abscissa given by |
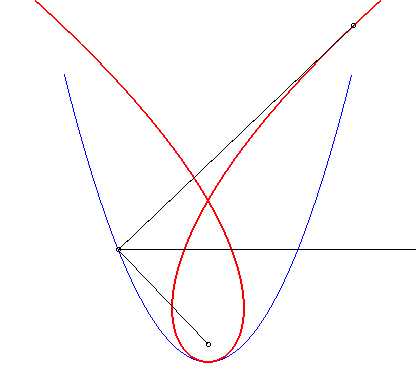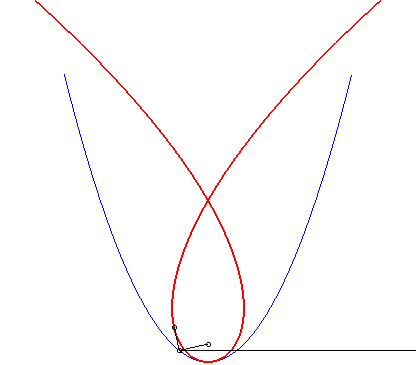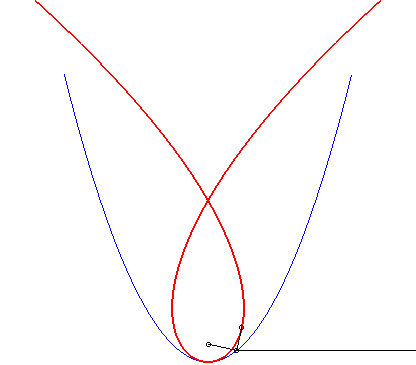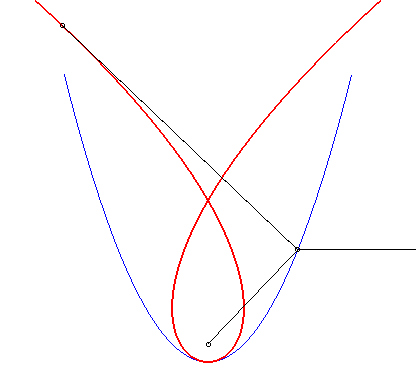
| The Tschirnhausen cubic is the negative pedal of the parabola with respect to its focus F, and the caustic by reflection of the same parabola for light rays perpendicular to the axis of the parabola (these two properties are linked, because of the property of the tangent to the parabola).
Likewise, it can be proved that the caustic by reflection of the parabola is a Tschirnhausen cubic irrespective of the direction of the rays, except when they are parallel to the axis of the parabola, in which case we get the focus. |
 |
| The Tschirnhausen cubic is also the caustic by reflection of the semicubical parabola for rays perpendicular to its axis. |
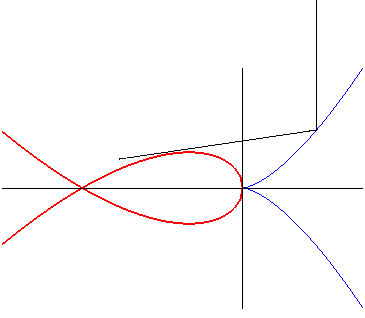 |
| Therefore, it is also the curve of a dog trying to catch its master, and going twice as fast as them. |
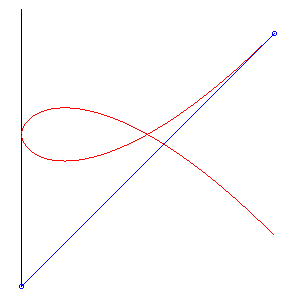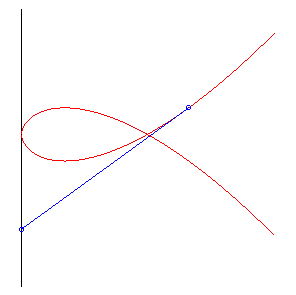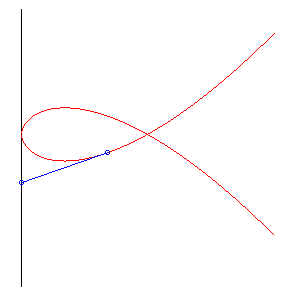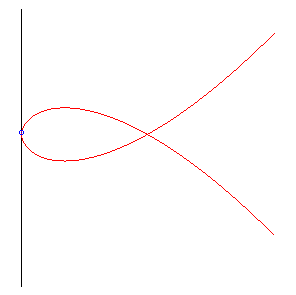 |
| It also is, up to scaling, the projection of the 3D parabola: |
 |
| If (D) is the line perpendicular to the symmetry axis, and its foot K is defined by |
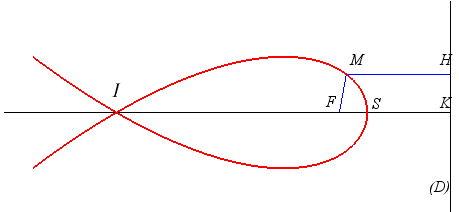 |
The Cartesian equation shows that the Tschirnhausen cubic is a special case of divergent parabola and the polar equation that it is a special case of sinusoidal spiral.
| The Tschirnhausen cubic is the roulette of the pole of a Norwich spiral rolling on a line. The line is then the double normal to the cubic. |
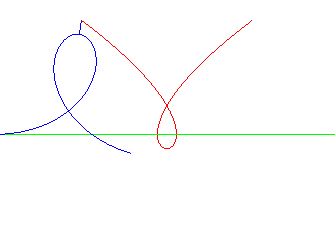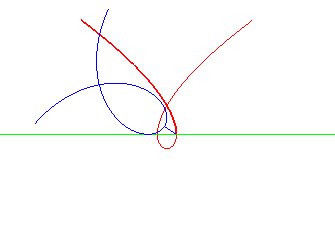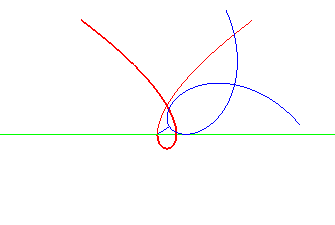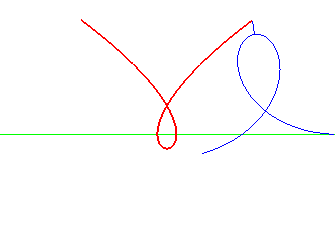 |
| We derive from this, thanks to a theorem of Mannheim, that the Tschirnhausen cubic is the curve on which travels a crab walking at the same speed as a point in linear motion, while facing it (see Duporcq curve). | 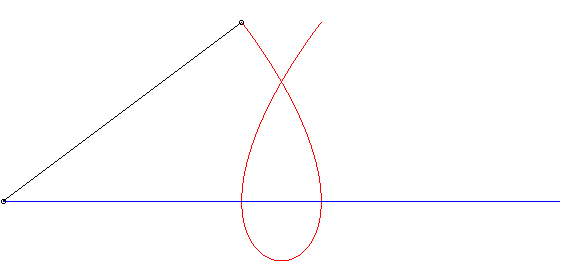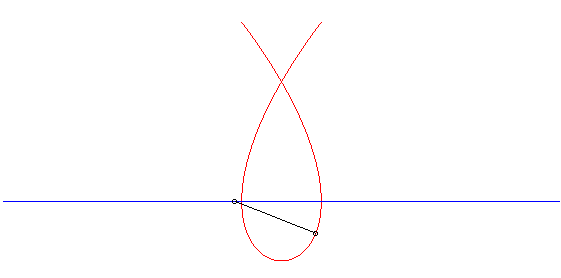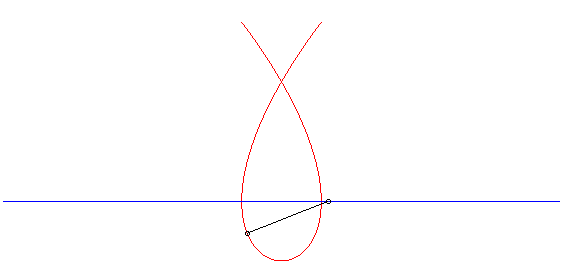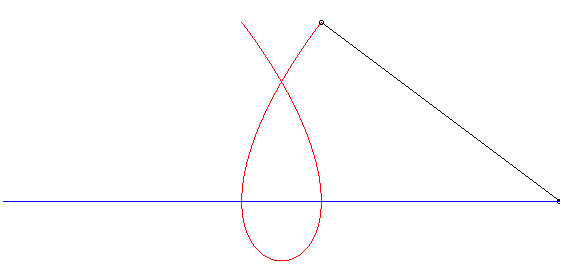 |
| And conversely, the roulette of the focus of a Tschirnhausen cubic rolling on a line is a parabola.
The glissette of this focus is a duplicatrix cubic. |
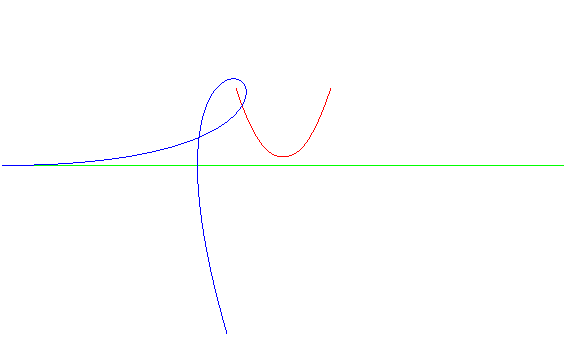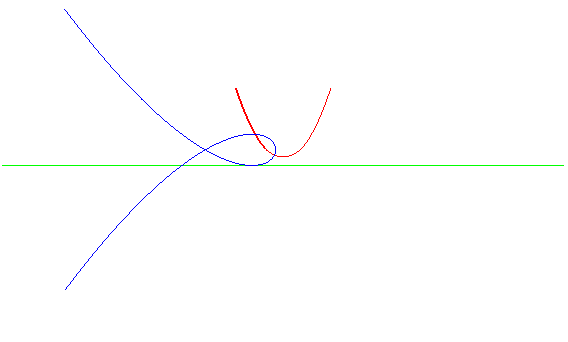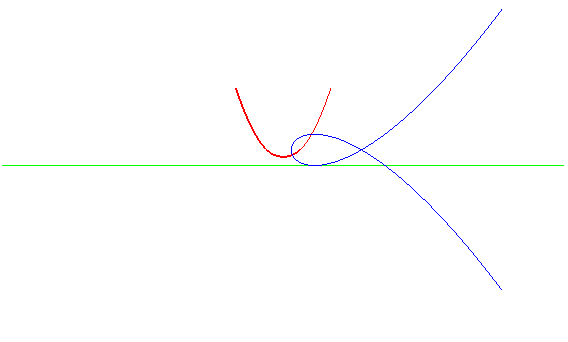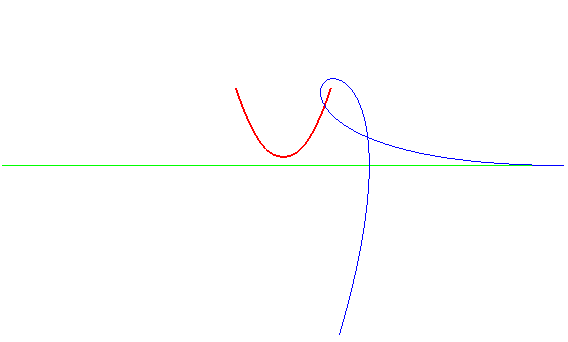 |
| Christophe Masurel looked for the "wheels" that, when rolling on a Tschirnhausen cubic, have their hub describe a linear trajectory (see at wheel-road couple); starting from the Tschirnhausen road k = 1: the wheel k = –1: the wheel k = 0: the wheel |
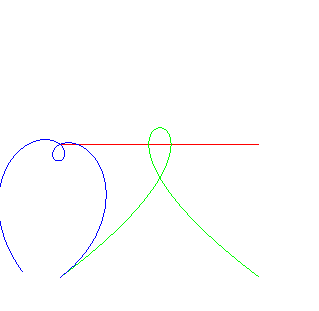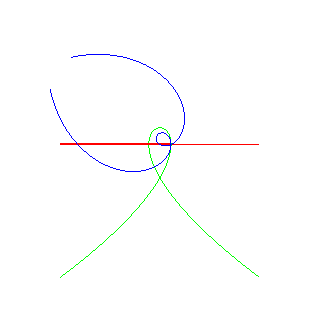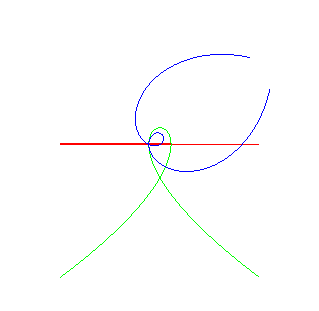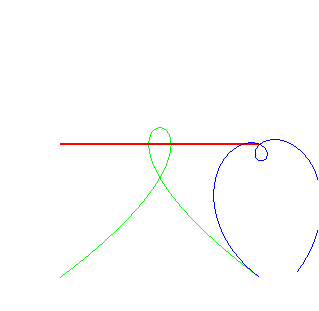
The rolling curve is a Galilean spiral, and roulette is the double normal. In this case, the curve Steiner-Habich theorem is a Norwich spiral. |
The rolling curve is a Norwich spiral
|
| When a Tschirnhausen cubic rolls on a line, its directrix envelopes an equal Tschirnhausen cubic the double normal of which is the base of the rolling motion.
This comes from the theorem: given a wheel-road couple, if the road rolls on a line, then the axis described by the hub of the associated wheel envelopes a curve that is the linear roulette of the hub; here, the road is a Tschirnhausen cubic, the axis its directrix, and the road a Norwich spiral. As it so happens that the linear roulette of the Norwich spiral is a Tschirnhausen cubic, we get the above property. |
 |
The Tschirnhausen cubic is a trisectrix (see Brocard Lemoyne III p.140).
The Enneper surface is the minimal surface a geodesic of which is the Tschirnhausen cubic.
The Tschirnhausen cubic, which also is the L'Hospital cubic, must not be mistaken for the L'Hospital quintic.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017