Polar equation of :   with n real. Complex equation: . Polar differential equation: . Curvilinear abscissa given by:  or . Polar tangential angle: . Pedal equation:  . Algebraic curve if and only if n is rational. In the case where n is a positive integer: Multipolar equation: , where  is a regular n-gon with radius a. Complex equation: . In the case where n = - m is a negative integer: Multipolar equation:  where  is a regular m-gon with radius a. Complex equation: . Length: ; area: .

The sinusoidal spirals are defined by their polar equation above.
When n is a positive integer, the sinusoidal spirals are the loci of the points for which the geometric mean of their distances to the vertices of a regular polygon is equal to the radius of this polygon; therefore, they are special cases of Cassinian curves with n poles.

When n is a negative integer, the sinusoidal spirals are the loci of the points M such that the mean of the angles formed by the lines joining the vertices of a regular polygon to M and a fixed direction is constant; therefore, they are special cases of stelloids.

and  are inverses of one another and the pedal of is .
The tangent can be easily constructed thanks to the relation: .
For n > 0, the curve is composed of a base pattern symmetrical about Ox obtained for : and transformed by all the rotations with angle for integral values of k; for n < 0, the base pattern has asymptotes.

When n is rational, we get the whole curve by p - 1 rotations of the base pattern for 1 £ k£ p - 1 where p is the numerator of n.
 

Examples for positive values of n:

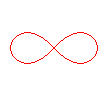
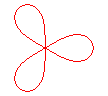
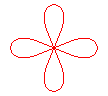
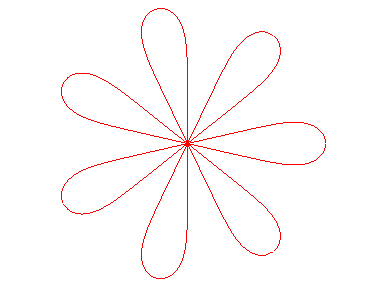
n = 1: circle	n  = 2: lemniscate of Bernoulli	n = 3: Kiepert curve	n = 4	n = 5
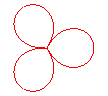
n = 1/2: cardioid	n = 3/2	n = 5/2	n = 7/2	n = 9/2
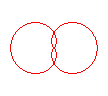
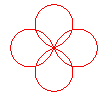
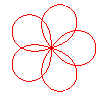
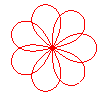
n  = 1/3: Cayley sextic	n = 2/3	n = 4/3	n = 5/3	n = 7/3
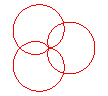
n = 1/4	n = 3/4	n = 5/4	n = 7/4	n = 9/4
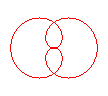
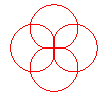
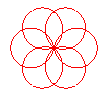
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5

Examples for negative values of n:

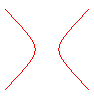
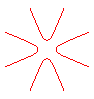
n = -1: line x = a	n  = -2: rectangular hyperbola	n = -3: Humbert cubic	n = -4	n = -5
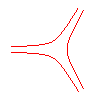
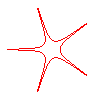
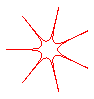
n =- 1/2: parabola y2 = 4a (a - x)	n = -3/2 Central negative pedal of the Kiepert curve	n = -5/2	n = -7/2	n = -9/2
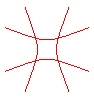
n  = -1/3: Tschirnhausen cubic	n = -2/3 central negative pedal of the rectangular hyperbola	n = -4/3	n = -5/3	n = -7/3
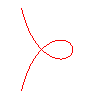
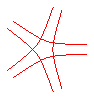
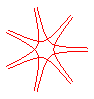
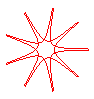
n = -1/4	n = -3/4	n = -5/4	n = -7/4	n = -9/4
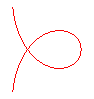
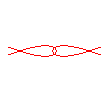
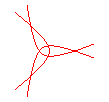
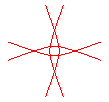
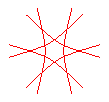
n = -1/5	n = -2/5	n = -3/5	n = -4/5	n = -6/5

The sinusoidal spiral of index n is the field line of the complex field (cf. the relation ):

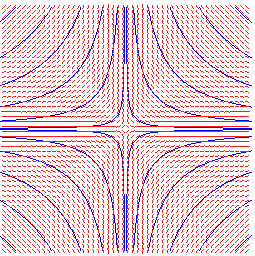
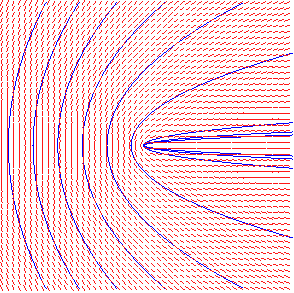
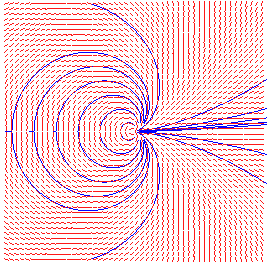
field lines of 1/z: hyperbolas of index -2	field lines of Öz: parabolas of index -1/2	field lines of z3/2 : cardioids of index 1/2
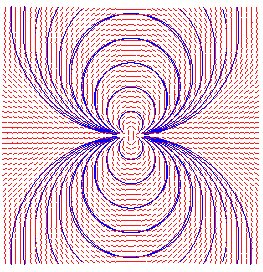
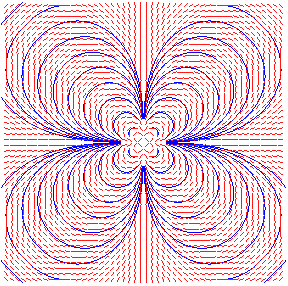
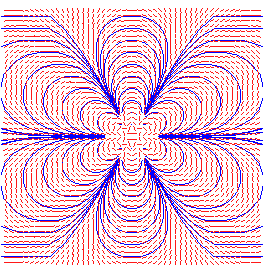
filed lines of z²: circles of index 1	field lines of z3: lemniscates of index 2	field lines of z4

See also the example n°6 of the orthogonal trajectories.

The sinusoidal spiral of index n is the trajectory of a massive point with mass m attracted by a central force with norm with , thrown in (a, 0) perpendicularly to Ox with a speed V₀ equal to . In the usual case of gravity (a = 2, i.e. n = -1/2), we get the parabola, and the speed V₀ is equal to the escape velocity (minimum speed needed for an massive point to go to infinity). The cases a = 1 or 3 (which would give n = -1 or 0) are excluded here; for the case a = 3, see at hyperbolic spiral, at epispiral, at logarithmic spiral and at Poinsot spiral.

The sinusoidal spirals are the planar projections of the asymptotic lines of the Plücker conoid.

The roulette of the pole of a sinusoidal spiral of index n rolling on a line is a Ribaucour curve of index 1+1/n.

© Robert FERRÉOL 2017