Fish curve: homemade name.

 

1st form Cartesian parametrization: . Cartesian equation: . Rational quartic.
2nd form (image by a rotation by , bringing the double point on O) Cartesian equation:  with and .

 

The fish curves are the projections on the planes passing by the axis Oy of Viviani's curve:.

 

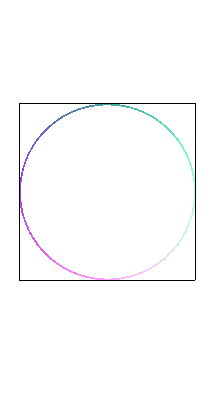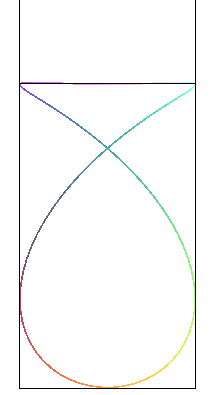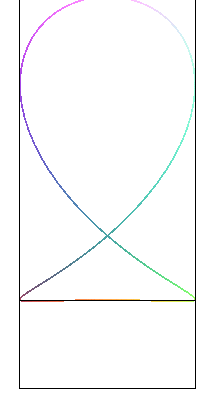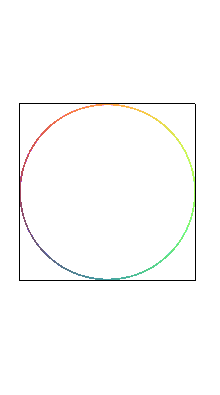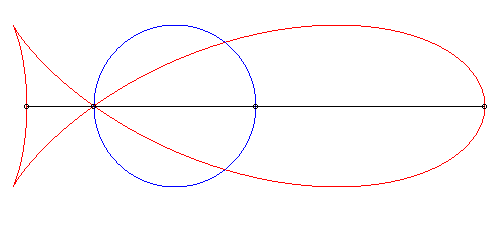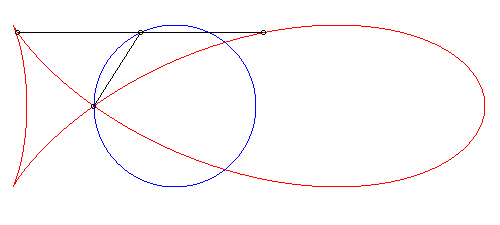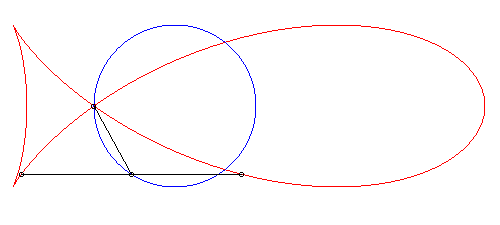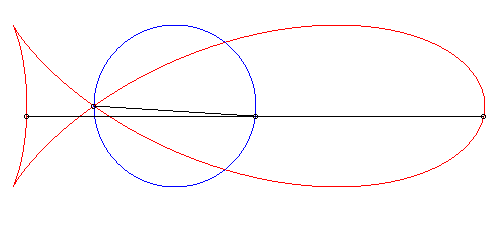
Given a circle (C), a fixed point O on this circle, a variable point N on this circle and the line (D) parallel to the diameter passing by O, the fish curve with parameter k is the locus of the intersection points between the circle with centre N and radius kON and the line (D). This construction is a generalisation of the strophoidal construction (case where k = 1).

In the case k = 2, i.e. q = 0, we get the torpedo.
Remark: in this latter case, if the functions sine and cosine are swapped in the parametrization, then we get the regular bifolium.
 

For 0 < k < 2, i.e. 0 < q < 1, the fish curve has 3 singularities forming a isosceles right triangle: A = (0, 0), B = (qa, 0), C = (0, qb) (frame of the 2nd form) which allows for the following geometrical interpretation: the fish curve is the solution to the problem of finding the locus of the points M such that the ratio of the algebraic area of the triangle (ABC) and that of the triangle (A'B'C') is equal to q/(1 – q), where A' B', C' are the centres of the circles circumscribed to (MBC), (MCA), (MAB)[François Duc, 2011]. The points B and C are cuspidal points iff , i.e. q = –1, and the fish curve then has a pointed back fin.

 

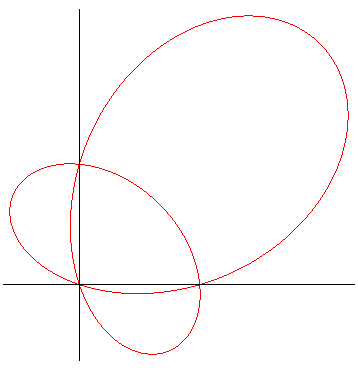The fish curves can also be obtained by the following construction (cf. the of naval superposition): given a fixed segment line [AB] of length 2L located at distance L of the centre of the circle with radius R, and a chord [PQ] of the circle, determining a central angle equal to p/2, with the vectors AB and PQ being oriented in the same direction when they are furthest from one another, the fish curve is the locus of the intersection points between the lines (AP) and (BQ). The relation between a,b,L,R is ; we get the fish with pointed fin for L=R.

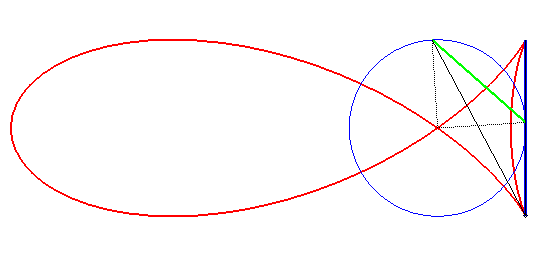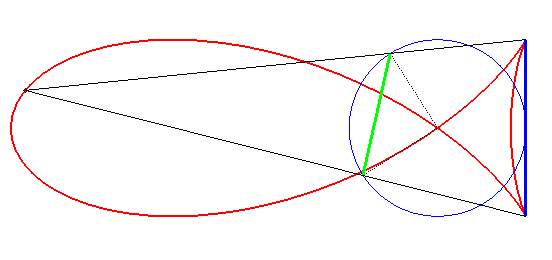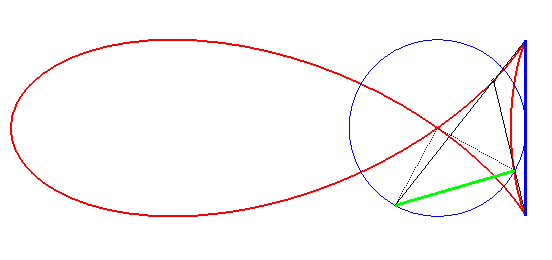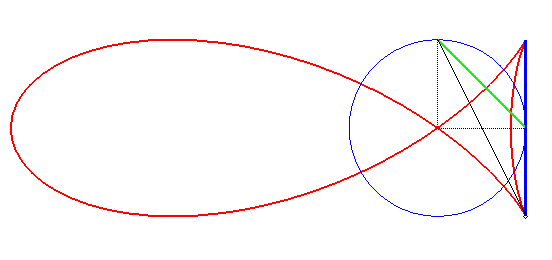If P and Q are swapped, we get a simple arc of a circle:

The "fish with pointed fin" is, up to scaling, the negative pedal of an ellipse of eccentricity with respect to its focus, and therefore, also, as it can be seen in the animation opposite, the locus of the equidistant points between the ellipse and the focus.

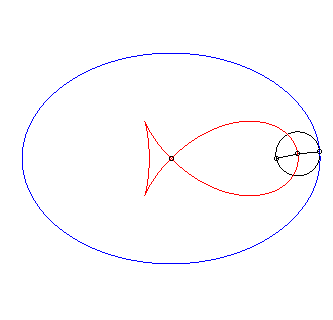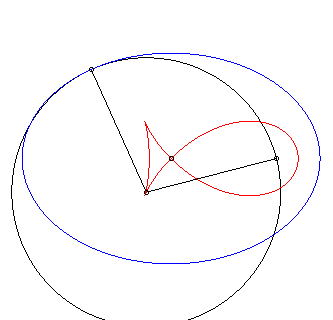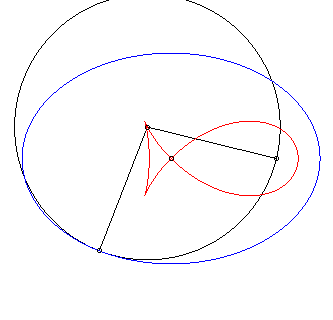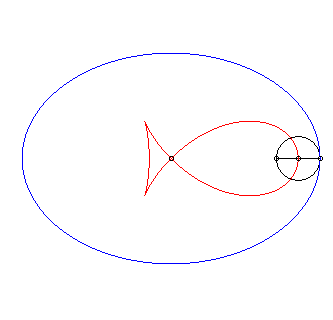Variation for Siamese fishes:.

© Robert FERRÉOL  2017