Notion étudiée par Tucker en 1864.

 

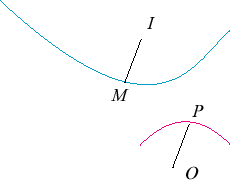
La radiale d’une courbe , associée à un point O fixe, est le lieu des points P définis par  où  est le vecteur joignant le point courant de  à son centre de courbure ; autrement dit c'est le lieu de l'extrémité du vecteur rayon de courbure, attaché à un point fixe.

 

Pour une courbe de départ :  de point courant  la radiale est l'ensemble des points . Paramétrisation cartésienne de la radiale : . Paramétrisation complexe : . Si la courbe de départ a pour équation intrinsèque 2 :, l'équation polaire de la radiale est :.

La radiale d'une courbe algébrique est une courbe algébrique de même degré que sa développée.

Exemples :
 

courbe de départ	radiale associée
cercle	cercle
ellipse	sextique d'équation soit  (Loria p. 308)
parabole	cubique duplicatrice
cycloïde(avec cercle roulant de rayon R)	cercle de rayon 2R
deltoïde	trifolium régulier
astroïde	trèfle à quatre feuilles
épicycloïde de paramètre q	rosace
hypocycloïde de paramètre q	rosace
chaînette d'égale résistance	droite
chaînette	kampyle d'Eudoxe
tractrice	kappa
développante de cercle	spirale d'Archimède
clothoïde	lituus
spirale logarithmique	spirale logarithmique
courbe de Ribaucourt d'indice k les cas k = -2, -1, et 2 redonnant les cas de la parabole, de la chainette et de la cycloïde ci-dessus.	courbe de Clairaut d'indice k-1
pseudo-spirale d'indice n les cas n = 0 , 1, et -1/2 redonnant les cas du cercle, de la clothoïde et de la développante de cercle ci-dessus.	spirale archimédienne d'indice

Voir une application des radiales dans les couples roue-route.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2012