COURBE DE RIBAUCOUR
Ribaucour
curve, ribaucoursche Kurve
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE DE RIBAUCOUR
Ribaucour
curve, ribaucoursche Kurve

| Problème posé par Jean Bernoulli en 1716,
résolu par Taylor en 1717 ; courbe étudiée ensuite
par Ossian Bonnet en 1844 et Ribaucour en 1880.
Albert Ribaucour (1845-1893) : ingénieur et mathématicien français. Voir aussi ce lien. |
| Equation différentielle du second ordre : Equation du premier ordre : Equation cartésienne : 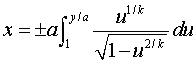 . .
Paramétrisation cartésienne : Courbe algébrique pour k entier impair. Abscisse curviligne donnée par : Rayon de courbure : |
|
Pour k entier >0, on peut prendre t quelconque ; la courbe est fermée pour k impair, périodique pour k pair. |
 |
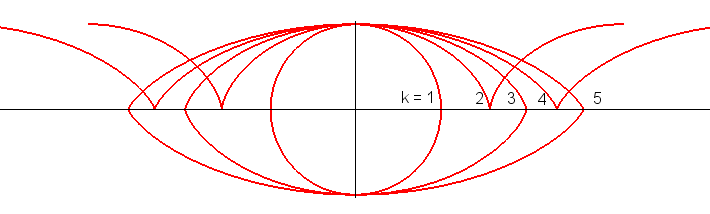
Pour k >0 et non entier, prendre |
Cas k = -1/4, -1/2, -1 (chaînette), -2 (parabole). |
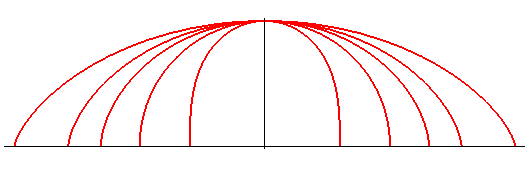
Pour k < 0 prendre |
| Une courbe de Ribaucour est une courbe dont tout point
M
vérifie |
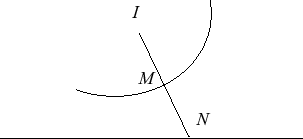 |
Autrement dit, en prenant Ox comme droite (D), ce sont les courbes telles que le rayon de courbure est proportionnel à la normale : Rc = – k N.
La courbe de Ribaucour d'indice k est aussi le
lieu du pôle de la spirale
sinusoïdale :
roulant sans glisser sur (D), avec
.
Elle est enfin la solution du problème de calcul
des variations consistant à déterminer les courbes rendant
extrémale l'intégrale
; c'est pourquoi on la retrouve aussi comme trajectoire d'un rayon lumineux
dans un milieu inhomogène : voir cette
page consacrée au principe de Fermat.
Cas particuliers :
| Indice de la courbe de Ribaucour | Nature de cette courbe | Indice
de la spirale sinusoïdale roulante |
Nature de cette spirale | figure | Intégrale dont la courbe de Ribaucour est l'extrémale | Interprétation |
| k = –2 | parabole de directrice (D) | n = –1/3 | cubique de Tschirnhausen, avec point traceur au foyer |
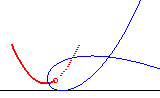 |
||
| k = –1 | chaînette de base (D) | n = –1/2 | parabole, avec point traceur au foyer |
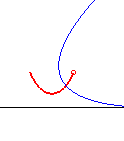 |
courbe joignant A à B rendant minimale l'aire de la surface engendrée par sa rotation autour de (D), surface qui est un caténoïde. | |
| k = –1/2 | voir dernière colonne | n = –2/3 | antipodaire centrale de l'hyperbole équilatère |
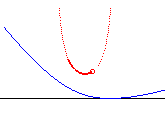 |
fil pesant homogène joignant A à B de moment d'inertie minimal | |
| k = 0 | point | n = –1 | droite | .... | .... | |
| k = 1/2 | Roulette de Sturm équilatère
ou lintéaire droite |
n = –2 | hyperbole équilatère |
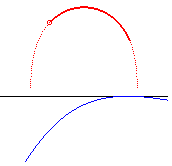 |
? | |
| k = 1 | cercle centré sur (D) | n infini | .... | géodésique dans le demi-plan de Poincaré | ||
| k = 3/2 | n = 2 | lemniscate de Bernoulli | voir l'animation ci-dessus | ? | ||
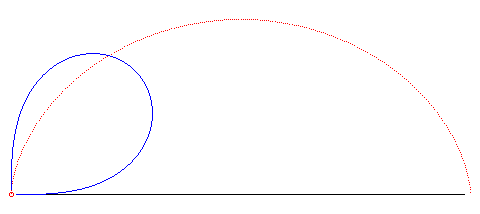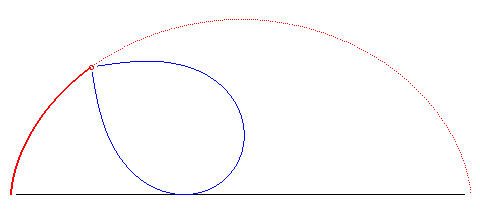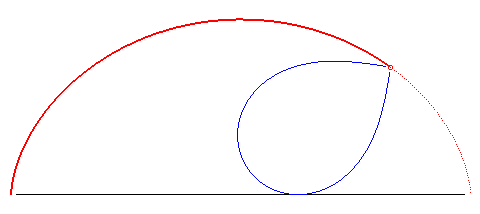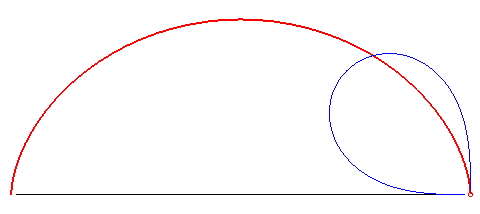
| k = 2 | cycloïde à points de rebroussement sur (D) | n = 1 | cercle, avec point traceur sur le cercle | 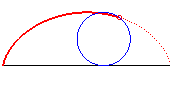 |
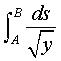 |
courbe brachistochrone |
| k = 3 | sextique
|
n = 1/2 | cardioïde, avec point traceur à la pointe | 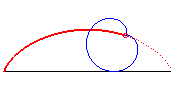 |
? | |
| k infini | droite | n = 0 | point | la droite est le plus court chemin d'un point à un autre... |
Nota : l'équation
montre que les courbes de Ribaucour pour k différent de 0,
peuvent être définies par
; on peut alors considérer que la courbe d'ordre 0 est la courbe
définie par
qui n'est autre que la chaînette
d'égale résistance.
Obtention des équations à partir des 3 définitions
ci-dessus :
| Démonstration à partir de la définition par la propriété des normales. | Démonstration à partir du roulement de la spirale sinusoïdale | Démonstration à partir du problème de calcul des variations |
| L' équation Rc = – k N s'écrit |
L'équation de la roulette du pôle de la
courbe d'équation polaire |
L'équation d'Euler-Lagrange appliquée à
l'intégrale |
La courbe de Mannheim d'une courbe de Ribaucour est une courbe de Ribaucour de paramètre k – 1.
La rotation d'une courbe de Ribaucour autour de l'axe
Ox
donne
une surface de révolution
dont les courbures principales sont proportionnelles en tous points.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2019