LINTÉAIRE DROITE
Right
lintearia, gerade Lintearia
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
LINTÉAIRE DROITE
Right
lintearia, gerade Lintearia

| Courbe étudiée par Euler
en 1744, Sturm
en 1840.
Autres noms : roulette de Sturm équilatère, élastique harmonique. |
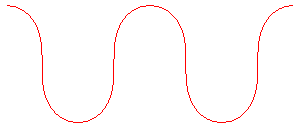
La lintéaire droite est la lintéaire
(ou courbe élastique) dont les points
d'inflexion sont orthogonaux à l'axe de la translation laissant
la courbe invariante.
| Équation différentielle : Paramétrisation cartésienne : Posant Abscisse curviligne : |
 |
Elle est solution de nombreux problèmes géométriques
ou physiques, dont voici deux exemples :
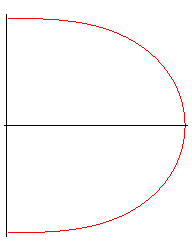
| La lintéaire droite est le lieu du centre d'une hyperbole équilatère roulant sans glisser sur une droite, d'où le nom de roulette de Sturm équilatère. |
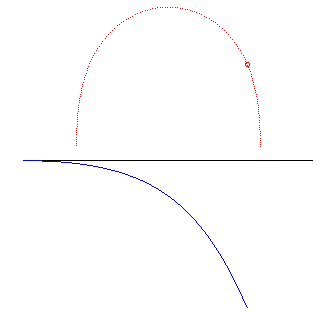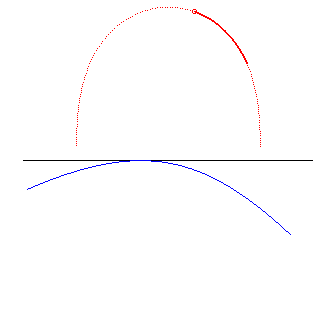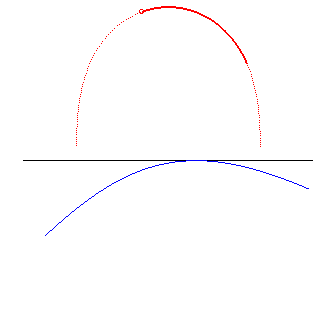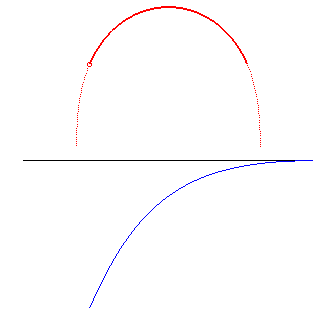 |
| Elle est aussi solution du problème de calcul
des variations suivant : trouver une courbe de longueur L donnée
joignant deux points A et B (variables) d'une droite (D)
(fixe), dont la rotation autour de la droite (D) engendre un solide
de volume maximal.
Notons que la courbe de longueur L donnée joignant deux points A et B (variables) d'une droite (D) (fixe), englobant une aire maximale est, elle, un demi-cercle. Cette propriété expliquerait la forme de la cornée ( voir cet article), et celui d'un ballon gonflable en Mylar (voir cet article). |
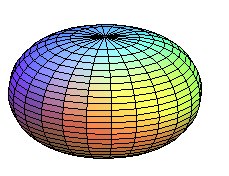 |
| Ballon composé de deux disques de Mylar qui sont cousus ensemble le long des bords et ensuite gonflé. Le ballon se gonfle, mais puisque la matière n'est pas extensible, le rayon initial du disque devient la longueur de la courbe de profil. |  |
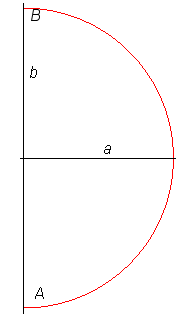
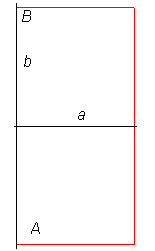
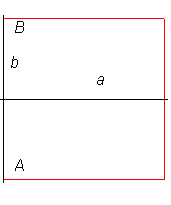
Ci-dessous, comparaison de la lintéaire droite,
du demi-cercle, d'un carré, et d'un rectangle, joignant A
à B.
On pose b = AB/2 et a la distance
à (AB) du point le plus éloigné de la courbe
joignant A à B.
L'aire englobée par la courbe est notée
S,
et le volume du solide de révolution V.
On remarquera que :
- le record de volume est obtenu avec
la lintéaire, mais parmi les rectangles, le record est obtenu avec
le carré.
- le record d'aire est obtenu avec
le demi-cercle, mais parmi les rectangles, le record est obtenu avec le
double carré.
| Lintéaire droite | Demi-cercle | Rectangle double carré | Carré |
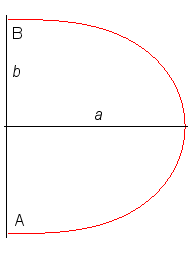 |
 |
 |
 |
| b = a I avec L = a J avec |
b = a
|
b = a
L = 4 a
|
b = a/2
L = 3 a
|
La lintéaire droite est obtenue pour k =
2 dans la famille des courbes
qui sont les profils des courbes
de révolution aux courbures proportionnelles.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2022