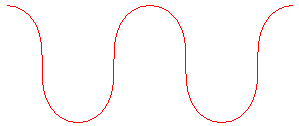
RIGHT LINTEARIA
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
RIGHT LINTEARIA

| Curve studied by Euler
in 1744, Sturm
in 1840.
Other names: rectangular Sturm roulette, harmonic elastic curve. |
The right lintearia is the lintearia (or elastic
curve) the inflexion points of which are orthogonal to the translation
axis.
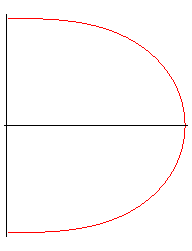
| Differential equation: Cartesian parametrization: With Curvilinear abscissa: |
 |
It is the solution of many geometrical or physical problems,
two examples of which follow:
| The right lintearia is the locus of the centre of a rectangular hyperbola rolling without slipping on a line, hence the name of rectangular Sturm roulette. |
 |
| It is also the solution to the following calculus of
variation problem: finding a curve with given length L joining two
(variable) points A and B on a (fixed) line (D), for
which the rotation around the line (D) generates the solid with
maximal volume.
Note that the curve with given length L joining two (variable) points A and B on a (fixed) line (D), delimiting the maximal area, is a semicircle. This property could explain the shape of the cornea (see this article), and that of an inflatable Mylar balloon (see this article.). |
 |
| Balloon composed of two Mylar disks sown together along the edges and then inflated. The balloon inflates, but since the material is not extensible, the initial radius of the disk becomes the length of the profile curve. |  |
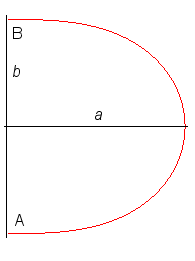
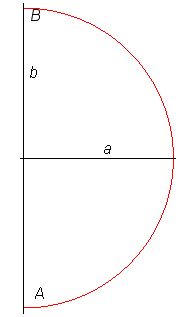
Below, a comparison of the right lintearia, the semicircle,
a square, and a rectangle, joining A to B.
We write b = AB/2 and a the distance
of the furthermost point on the line joining A and B to (AB).
The area delimited by the curve is noted S, and
the volume of the solid of revolution V.
We will see that :
- the maximal volume is obtained with
the lintearia, but among the rectangles, the maximum is obtained with the
square.
- the maximal area is obtained with
the semicircle, but among the rectangles, the maximum is obtained with
the double square.
| Right lintearia | Semicircle | Double square rectangle | Square |
 |
 |
 |
 |
| b = a I with L = a J with |
b = a
|
b = a
L = 4 a
|
b = a/2
L = 3 a
|
The right lintearia is obtained for k = 2 in the
family of curves
which are the profiles of the curves
of revolution with proportional curvatures.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2022