k > 1	0 < k < 1	-1 < k < 0	k < -1

 

Surface studied by Wolfgang Kühnel in 1999 (Differential Geometry, p. 95)

 

Cylindrical parametrization: 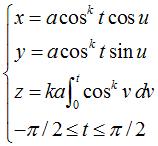, cartesian parametrization: . Differential equation:  or  where . Parallel and meridian radius of curvature: .

It's about the rotation surface for wich both principal radius of curvature (or both prinipal curvatures, or again mean curvature and total curvature) are proportionnal at each point  - see the notations.

The meridian radius of curvature of a rotation surface being
that of the profile of this surface, and the parallel radius of curvature joining the point M of the surface at the point of intersection of the normal with  the axis, the profiles of
the surfaces studied here are only curves whose radius of
curvature is proportional to the normal (or such that the quotient MI / MN is constant where I is the center of curvature), in other words, the curves of Ribaucour.
 

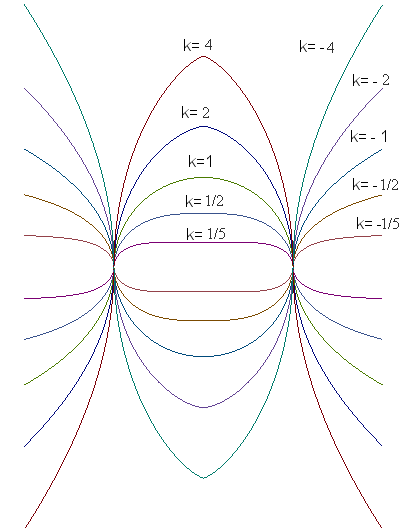
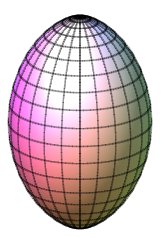
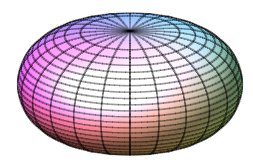
Various cuts by a plane passing through the axis ;  for k = 1 we get the circle, for k = 2 the cycloid, for k =1/ 2 the right lintearia,  for k = –1 the catenary., and for k = – 2 the parabola (of directrix Oz).	Half-surfaces with k = 2, k = 1 (sphere), k = 1/2, et k  = 1/5. Note that the relation  is not valid for the intersection point with the axis, that is singular for k > 1/2 and a level point for .	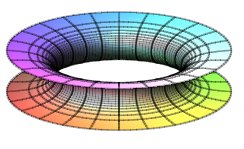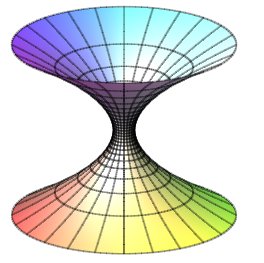Half-surfaces with k = – 1/2 (Flamm's paraboloid) and k = –1 (catenoid).

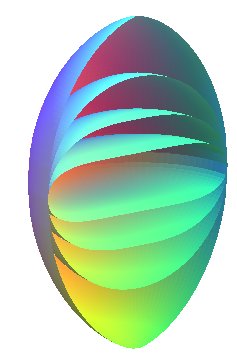Compare with rotation surfaces with constant gaussian curvature  (that is, whose two curvatures are inversely proportional).
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2019