CHAÎNETTE D’ÉGALE RÉSISTANCE
Catenary
of equal strength, Kettenlinie gleichen Widerstandes
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CHAÎNETTE D’ÉGALE RÉSISTANCE
Catenary
of equal strength, Kettenlinie gleichen Widerstandes
| Courbe étudiée par Finck
et Bobillier en 1826 et Coriolis
en 1836.
Autres noms : chaînette de Coriolis, longitudinale, courbe du log cosinus. |
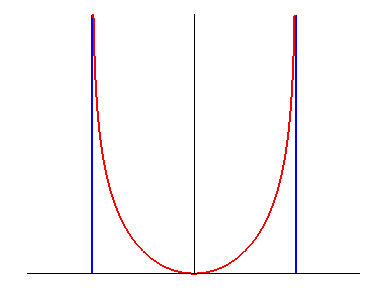
La chaînette d'égale résistance se
différencie
|
Equation diférentielle :  .
Équation cartésienne :  .
Courbe transcendante. Abscisse curviligne :  (rappel
: sec = 1/cos)
Angle tangentiel cartésien :  .
Rayon de courbure :  .
Équation intrinsèque 1 :  .
Équation intrinsèque 2 :  .
Aire entre limité par Ox et les asymptotes :  .
Courbe transcendante. |
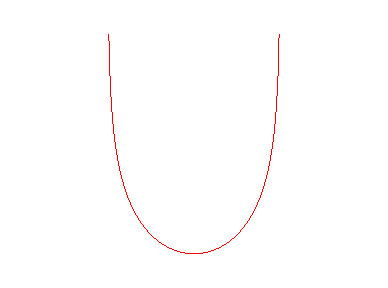
La chaînette d'égale résistance est
la forme prise par un fil pesant flexible inextensible suspendu entre 2
points, quand la masse linéique (c'est-à-dire, en pratique,
l'épaisseur du fil) est proportionnelle à la tension.
Un tel fil n'offre donc pas plus de chance de rupture
en un point qu'en un autre.
Cette courbe, renversée, représente le profil d'une voûte
sans surcharge (Brocard) ??
Avec les notations de la figure ci-dessus (
= tension du fil en M, m = masse linéique
du fil) , écrivons que la somme des forces en M est nulle
:  .
Ceci se simplifie en  ,
qui par intégration donne 
; on en déduit 
et  d'où 
et comme on veut 
donc  ,
on obtient l'équation différentielle : 
fournissant l'équation cartésienne ci-dessus. |
 |
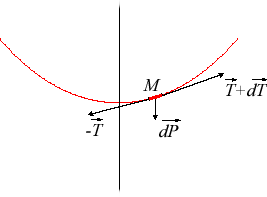La masse linéique est alors égale à 
,
ce qui détermine l'épaisseur d'un tel fil.
La formule 
montre que la projection du segment rayon de courbure sur l'axe des x
a une longueur constante ; cette propriété est caractéristique
de la chaînette d'égale résistance.
La chaînette d'égale résistance est
aussi le cas particulier
k = 1 de la famille des courbes d'équation
intrinsèque 1 :  ,
courbes n'ayant pas de nom connu, mais ayant pour paramétrisation
: 
Ci-contre une animation pour k allant de 0 à 6, avec arrêts à k =1 (chaînette d'égale résistance), k = 2 (courbe des forçats), et k = 4. |
 |
Voir aussi à courbe de Ribaucour, dont la chaînette d'égale résistance peut être considérée comme un cas particulier.
La radiale de cette
courbe est la droite x = a et sa courbe
de Mannheim une chaînette.
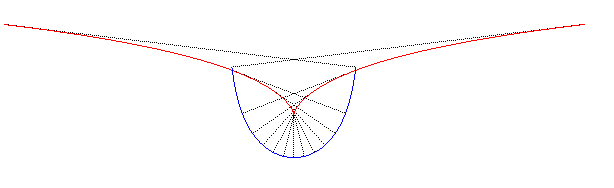
La développée
de la chaînette d'égale résistance est la courbe de
paramétrisation :  |
 |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL, Jacques MANDONNET 2010