Ophiuride

Courbe étudiée par Uhlhorn en 1809.
Du grec ophis "serpent" et oura "queue".

Équation polaire :

.
Équation cartésienne :

.
Cubique circulaire rationnelle à point double.

Comme toute cubique circulaire rationnelle, les ophiurides possèdent trois définitions géométriques. Ce sont :
- les cissoïdales de pôle O d'un cercle (C) passant par O et d’une droite (D) dont la symétrique par rapport à O passe par A diamétralement opposé à O (ici A(a, b) et (D) : x = – a).

- les podaires d’une parabole par rapport à un point de sa tangente au sommet (ici la parabole de foyer A et de tangente au sommet Oy).

- des inverses d’hyperbole par rapport à l'un de ses points (ici de l'hyperbole

, le cercle d'inversion étant le cercle (O, r)).

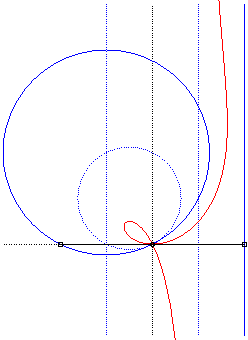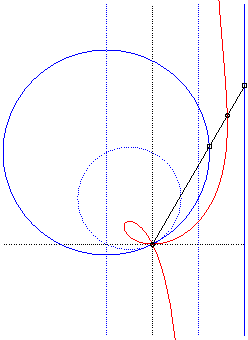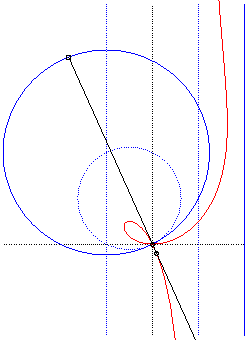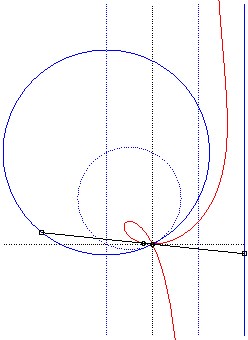
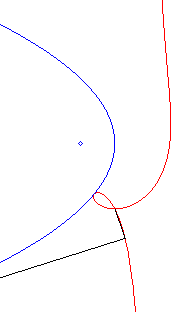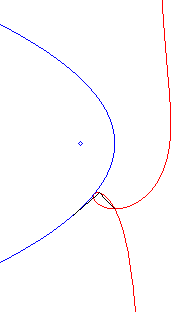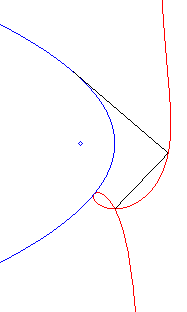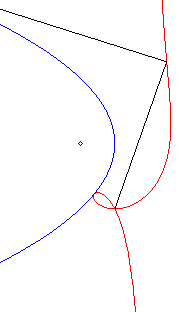
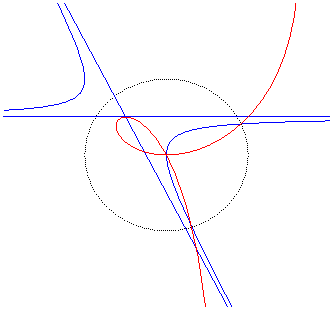
Remarquons que l'ophiuride droite n'est autre que la cissoïde droite.

des ophiurides réelles !

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres