LIGNE DE CHAMP MAGNÉTIQUE INDUIT PAR UNE SPIRE
CIRCULAIRE ET PAR UN DIPÔLE MAGNÉTIQUE
Magnetic
field line, magnetische Feldlinie
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
LIGNE DE CHAMP MAGNÉTIQUE INDUIT PAR UNE SPIRE
CIRCULAIRE ET PAR UN DIPÔLE MAGNÉTIQUE
Magnetic
field line, magnetische Feldlinie

| Voir aussi cet article de l'union des physiciens. |
| Le potentiel vecteur du champ magnétique créé
par un courant d'intensité I parcourant la courbe Pour une spire circulaire et celle des lignes orthogonales : |
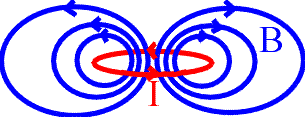
Les courbes étudiées ci-dessus sont les lignes de champ magnétique créé par un courant continu circulant dans la spire circulaire de rayon a centrée en O dans le plan xOz, et leurs trajectoires orthogonales :
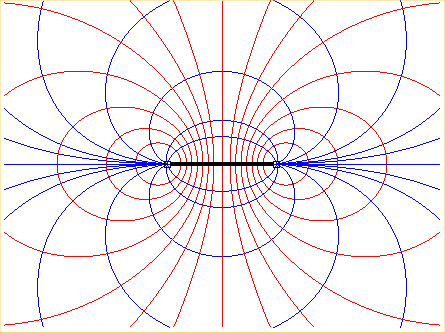
Lorsque le point M est éloigné de
la spire, celle-ci est appelée un dipôle magnétique
; en utilisant le développement : ,
on obtient
le champ magnétique approché :
Voir une autre démonstration à romain.bel.free.fr/agregation/Lecons/LP27.doc
Les lignes de champ sont alors des oeufs
doubles : ,
et les lignes orthogonales, des courbes
du dipôle, d'équation polaire
.
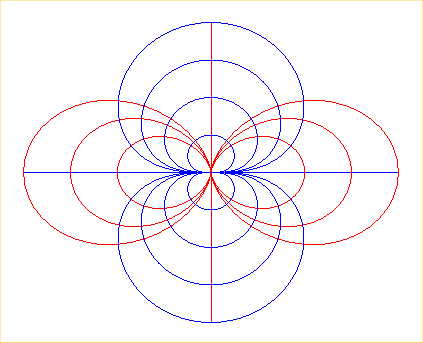
en rouge, les lignes de champ magnétique créé
par un dipôle, et en bleu les lignes orthogonales.
Remarque : si l'on remplace la spire par deux fils "infinis" parcourus par des courants contraires, les lignes de champ forment un faisceau de cercles à points de base l'intersection des fils avec le plan :
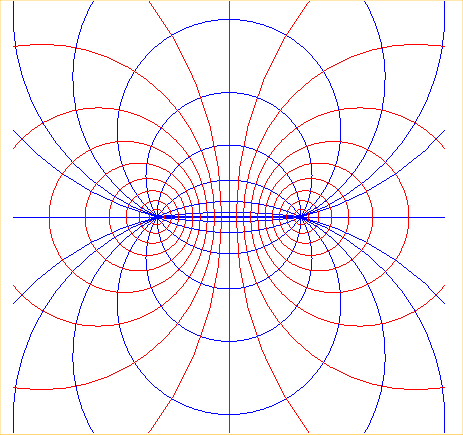
Voir d'autres lignes de champ ici
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL, Alain ESCULIER, 2003