où P, Q et R sont trois polynômes à
coefficients réels dont le maximum des degrés est 6.
En remplaçant t par
,
on obtient une paramétrisation trigonométrique : 
.| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SEXTIQUE RATIONNELLE
Rational
sextic, rationale Sextik
Les sextiques rationnelles
sont les sextiques de genre
nul, ayant donc entre un et dix points singuliers faisant diminuer le genre
de 10 (dans le plan projectif complexe).
| Paramétrisation cartésienne :
où P, Q et R sont trois polynômes à
coefficients réels dont le maximum des degrés est 6.
En remplaçant t par ,
on obtient une paramétrisation trigonométrique : . |
La plupart des sextiques rationnelles remarquables font
partie de la famille des courbes rationnelles de degré £
6,
bornées, et d'axe de symétrie
Oy,
de paramétrisation 
, comme on le constatera ci-après.
Exemples de sextiques rationnelles :
1) Première famille : 
- le quadrifolium
et ses conchoïdes
: 
(a
= 0 : quadrifolium, a = 1 : trisectrice
de Ceva , a = 2 : oeuf
double : a > 2 : cacahuète)
- les épitrochoïdes
de paramètre q = 2: 
(a = 1 : folium de
Dürer , a = 3 : néphroïde).
- les hypotrochoïdes
de paramètre q = 4: 
(a = 1 : quadrifolium , a
= 3 : astroïde ).
- la cornoïde
: 
- la croix
de Malte : 
- La double
goutte d'eau :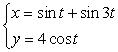 
- les courbes
de Talbot : 
.
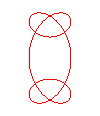
- une somme de deux trèfles
: 
Par ordre d'apparition : a = 0 : quadrifolium a = pi/4 : croix de Malte a= pi/2 : double goutte d'eau a = 3pi/4 : oeuf double a = pi-arctan(1/2) : folium de Dürer a= pi-arctan(1/3) : courbe ressemblant à la cornoïde |
 |
Ces courbes sont les projections sur les plans contenant Oy de la courbe gauche :  |
 |
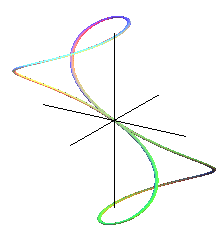2) Deuxième famille :
avec b ou e non nuls.
- le folium
de Dürer et ses conchoïdes
: 
(a
= 0 : folium de Dürer, a = 1 : néphroïde
de Freeth )
- les épitrochoïdes
de paramètre q = 1/2: 
.
- les hypotrochoïdes
de paramètre q = 5/2 (étoiles à 5 branches)
: 
.
- la sextique
de Cayley : 
- une courbe
de Lissajous :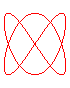 
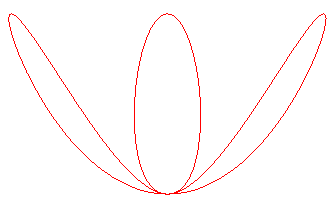
- une jolie sextique avec un point triple à tangentes
confondues, faisant partie des vasques
:  |
 |
- une autre, qui est indécomposable, et
semble pourtant se décomposer en un cercle et un huit : 
(le vrai cercle en vert). |
 |
3) Autres exemples.
- le moulin
à vent : 
- le noeud
de papillon : 
- les scarabées
: 
(dont
le quadrifolium : 
)
la courbe suivante semble elle aussi se décomposer,
en un cercle et une cardioïde :
 .
Cette courbe est associée aux triangles dont une hauteur, une médiane et une bissectrice sont concourantes (triangles considérés par E. LEMOINE en 1885 dans mathesis) : si l'on fixe le sommet de la hauteur en (0,1) et le sommet de la médiane en (0,0), cette courbe est le lieu du troisième sommet d'un tel triangle. Le lieu du point de concours est une septique. |
 |
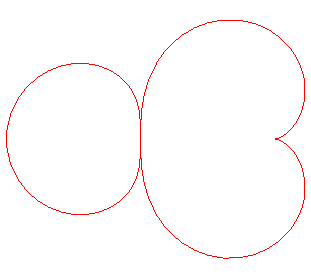| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2021