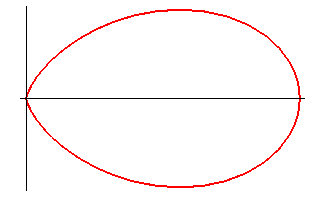
Contrairement aux apparences, il y a une tangente (verticale) en O ;  par contre, le rayon de courbure y est nul alors qu'il ne l'est pas à l'autre extrémité (cf. l'oeuf et sa développée ci-dessous).

Équation polaire :  (courbe de Clairaut). Équation cartésienne: . Paramétrisation cartésienne rationnelle : . Quartique circulaire rationnelle. Rayon de courbure : . Longueur : . Aire : . Volume du solide de révolution (que l'on peut dénommer ovoïde de Képler) obtenu en faisant tourner le folium autour de son axe : .  Aire latérale : .

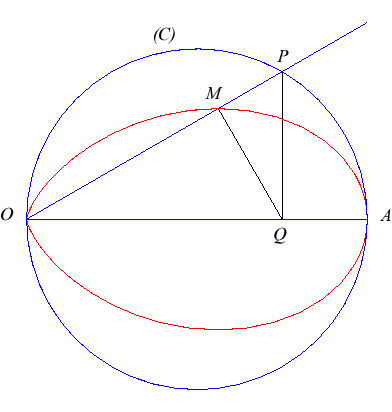
Étant donné un cercle (C) de diamètre [O A], et un point variable P décrivant (C), le folium simple est le lieu du projeté M sur (D) du projeté Q sur (OA) de P.
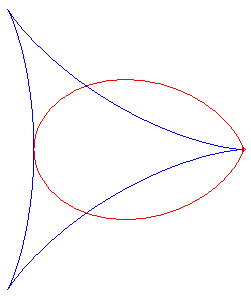
Le folium simple est la podaire de la deltoïde par rapport à un de ses points de rebroussement ; c'est donc un cas particulier de bifolium et de folium droit, l'autre étant le bifolium régulier.
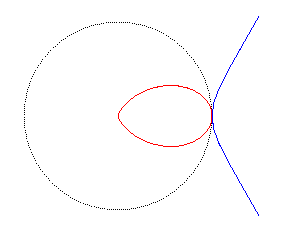
C'est aussi l'inverse de la cubique duplicatrice par rapport à son point isolé.

Comparer avec l'oeuf double ( au lieu de ) et regarder d'autres oeufs à ovoïde.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2011