Surface de Boy

SURFACE DE BOY
Boy surface, boysche Fläche

Cliquer sur ce lien pour une applet permettant de manipuler la surface

Surface étudiée par Werner Boy en 1902, Bernard Morin en 1978, Jean-Pierre Petit et Jérome Souriau en 1981.
Werner Boy (1879 - 1914) : élève de Hilbert (voir ici ce qu'en raconte Jean-Pierre Petit).
Voir aussi : fr.wikipedia.org/wiki/Surface_de_Boy
et l'article de Jean-Pierre Petit : www.cs.berkeley.edu/~sequin/CS294/IMGS/boysurface.htm

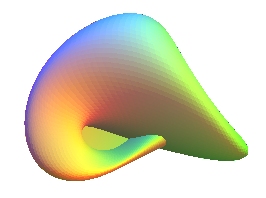
Paramétrisation cartésienne d'Apéry (1986), utilisée pour les images ci-dessus :
avec .
Paramétrisation cartésienne de Bryant-Kusner (1987) :
où , ,, avec
Paramétrisation cartésienne de Morin-Apéry (1987), faisant passer de la surface romaine (k = 0) à la surface de Boy (k = 1) :
où .
Surface algébrique de degré 6.

La surface de Boy a été découverte suite à la recherche d'un modèle dans du plan projectif qui ne possède pas d'autre singularité que des auto-intersections le long desquelles les différentes nappes ont un plan tangent bien défini (la surface romaine et le bonnet croisé,qui étaient connus, possèdent des points cuspidaux).
Boy a décrit sa surface de façon conceptuelle, et ce n'est qu'en 1981 que J.P. Petit et J. Souriau en ont trouvé une paramétrisation.

Autant le bonnet croisé est obtenu en tordant le bord d'un disque en une courbe à un croisement jusqu'à faire coïncider les deux parties (de sorte que les points opposé du bord du disque coïncident),...

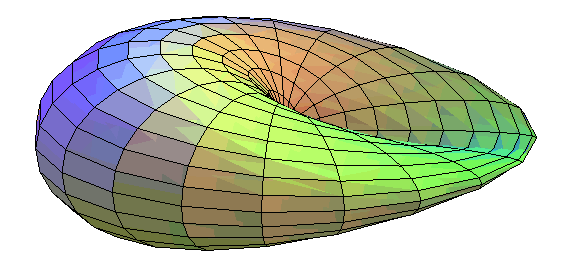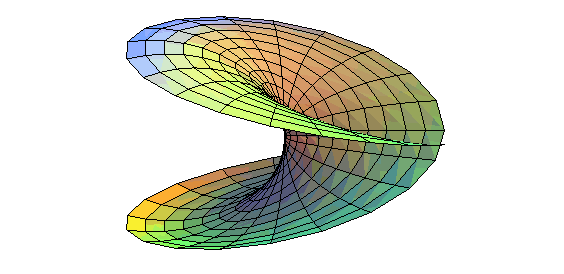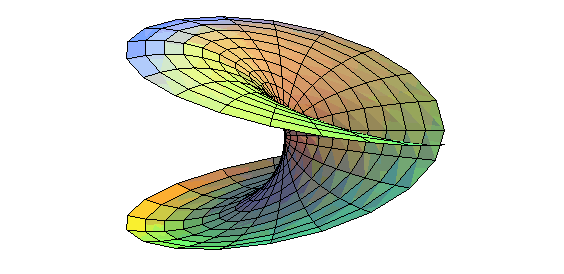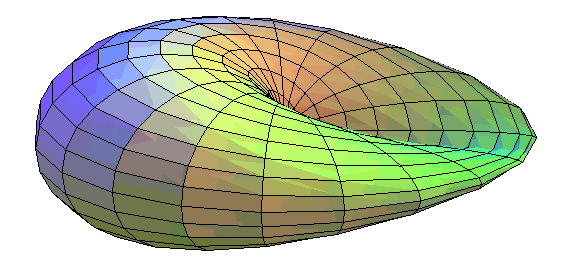...autant la surface de Boy est obtenue en tordant un disque en une courbe à trois croisements, jusqu'à faire coïncider 2 à 2 les 6 parties (d'où la symétrie d'ordre 3 de cette surface)

Ci-contre, diverses animations expliquant la construction (paramétrisation de Bryant-Kusner):

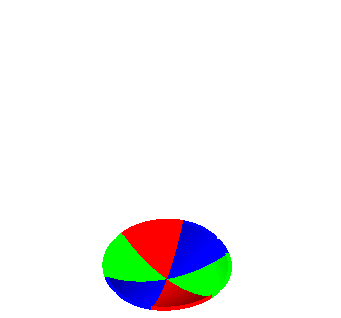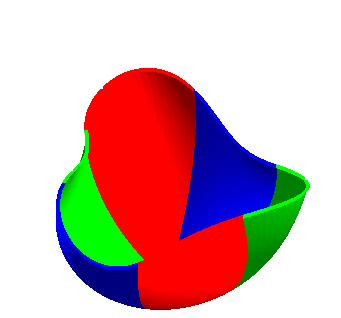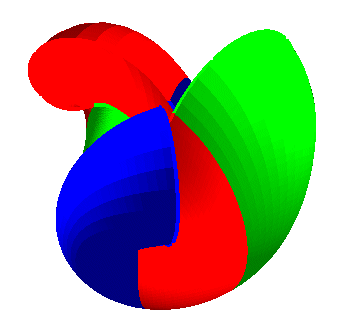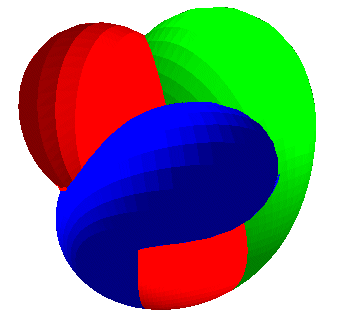La surface de Boy possède 3 orifices conduisant à des tunnels se rejoignant dans la partie centrale.
Suivre un chemin pour comprendre que la surface n'a qu'une face.

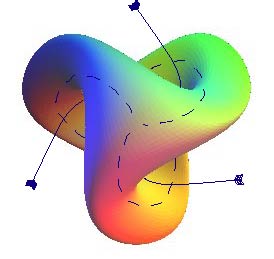Ci-contre, animation utilisant la paramétrisation de Morin-Apéry, montrant la déformation de la surface romaine en la surface de Boy ; les 3 points cuspidaux de la surface romaine disparaissent à partir de la valeur .

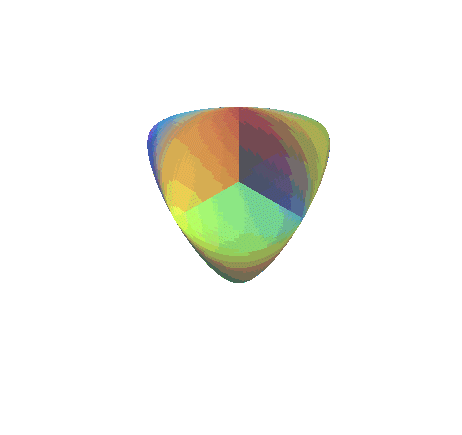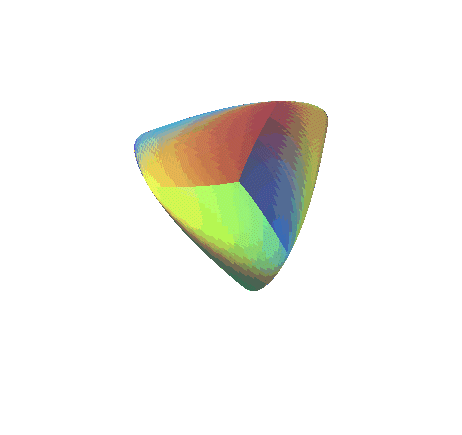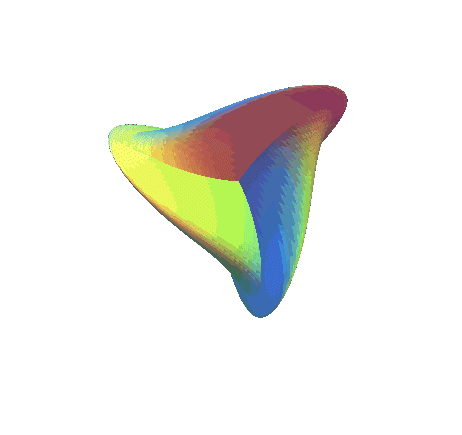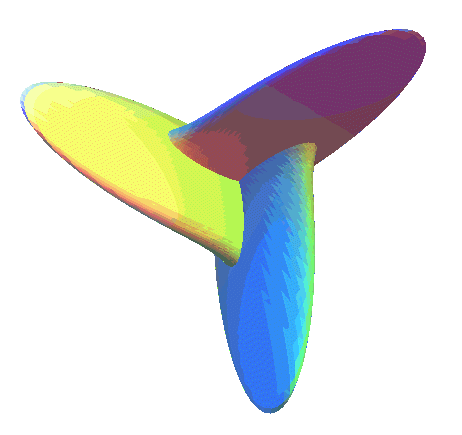La courbe d'auto-intersection de la surface de Boy est un trifolium tordu ; les 3 tangentes au point triple sont 2 à 2 orthogonales (et donc aussi les trois plans tangents à la surface en ce point triple).
Voir aussi à quadrifolium.

La paramétrisation ci-dessus de Morin-Apéry en fait une surface algébrique de degré 6, et on a montré qu'on ne pouvait pas abaisser ce degré sans faire apparaître de point cuspidal (la surface romaine et le bonnet croisé sont des quartiques).

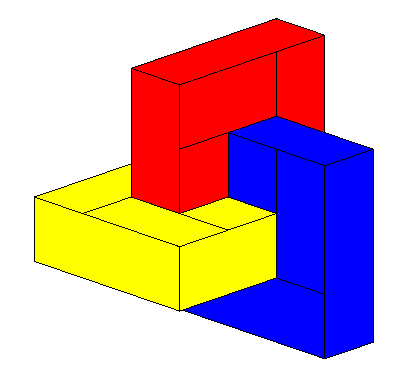
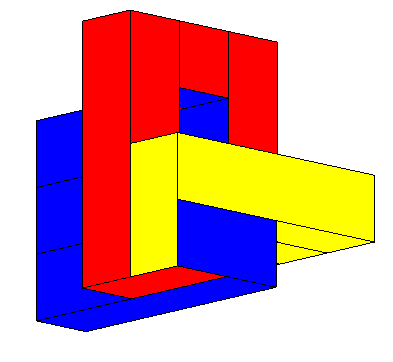
Voici un modèle de la surface de Boy sous forme de réunion de rectangles joints.
La courbe d'auto intersection est formée de 3 carrés situés dans 3 plans 2 à deux perpendiculaires.
Certains rectangles contigus étant coplanaires, ce modèle devrait être déformé pour devenir réellement un polyèdre, mais il existe un vrai polyèdre (généralisé) qui est un modèle de la surface de Boy : le polyèdre de Brehm.

Si l'on peint la surface de Boy, la pellicule de peinture (qui est d'un seul tenant puisque cette surface est unilatère) obtenue est une immersion de la sphère (car le revêtement à deux feuillets du plan projectif est la sphère); c'est la raison pour laquelle la surface de Boy a été utilisée comme étape centrale du retournement de la sphère : voir par exemple, ce texte de Pour la Science.
Voir aussi la surface de Morin.

photo d'une sculpture de surface de Boy dans une université allemande

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres

Autant le bonnet croisé est obtenu en tordant le bord d'un disque en une courbe à un croisement jusqu'à faire coïncider les deux parties (de sorte que les points opposé du bord du disque coïncident),...
...autant la surface de Boy est obtenue en tordant un disque en une courbe à trois croisements, jusqu'à faire coïncider 2 à 2 les 6 parties (d'où la symétrie d'ordre 3 de cette surface)