POLYÈDRE DE BREHM
Brehm's polyhedron, Brehmsches Polyeder
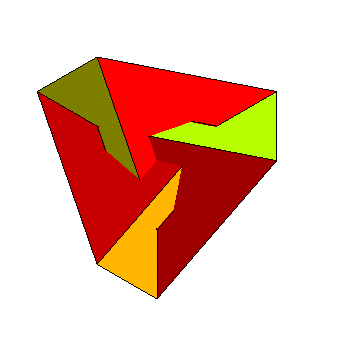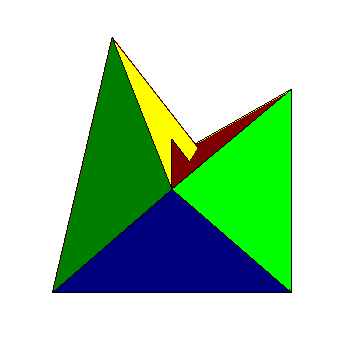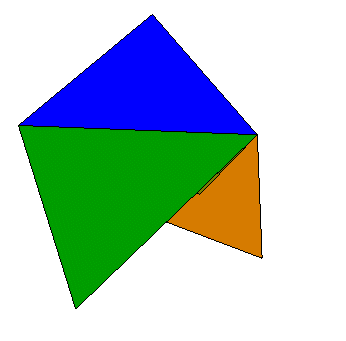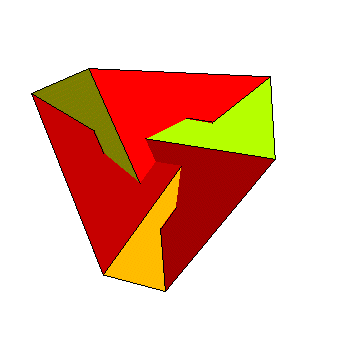
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
POLYÈDRE DE BREHM
Brehm's polyhedron, Brehmsches Polyeder
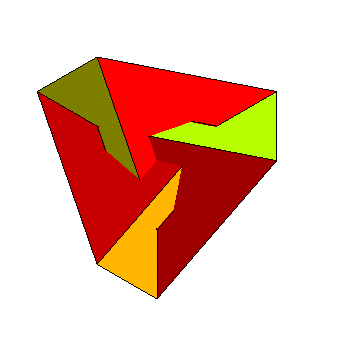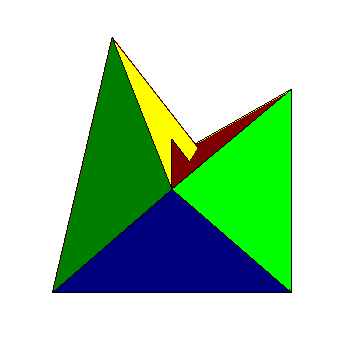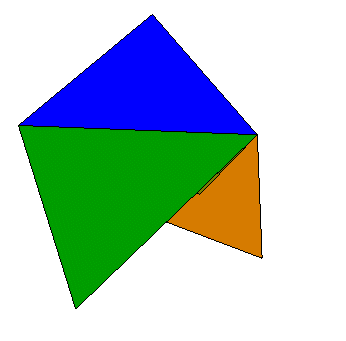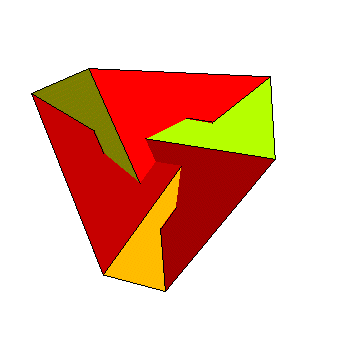
| Ulrich
Brehm : Mathématicien allemand.
Polyèdre construit en 1988. |
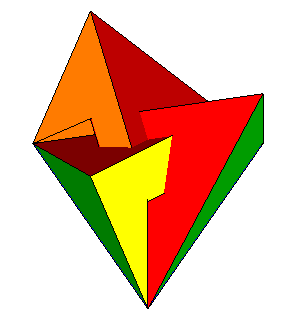
Le polyèdre de Brehm est un polyèdre (généralisé) à 10 faces (c'est donc un décaèdre), 9 sommets et 18 arêtes, répondant à la question de construire un modèle de la surface de Boy possèdant un nombre minimal de sommets (on peut montrer que le nombre de sommets ne peut être inférieur à 9).
Sa caractéristique d'Euler-Poincaré est S - A + F = 1, qui est bien celle du plan projectif.
Le polyèdre est formé de
| 3 faces pentaédriques isométriques, formant
un ruban de Möbius
|
3 faces triangulaires isométriques, se coupant
un un point triple
 |
et 3 autres faces triangulaires isométriques,
jointes par une base triangulaire également.
 |
|
|
 |
|
Voir sur cette page un modèle polyédrique minimal de la surface de Boy dont les faces sont des triangles.

Animation réalisée par Alain Esculier ; anaglype à regarder avec des lunettes rouge à gauche et bleu à droite.
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2013