

| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
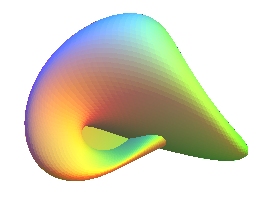
BOY'S SURFACE
 |
 |
 |
| Surface studied by Werner Boy in 1902,
Bernard
Morin in 1978, Jean-Pierre Petit and Jerome Souriau in 1981.
Werner Boy (1879 - 1914) : student of Hilbert (see here what Jean-Pierre Petit says about him). See also: en.wikipedia.org/wiki/Boy%27s_surface and Jean-Pierre Petit's article: www.cs.berkeley.edu/~sequin/CS294/IMGS/boysurface.htm |
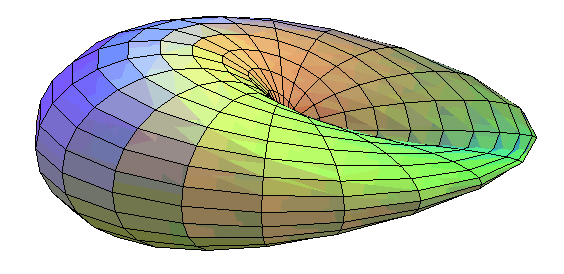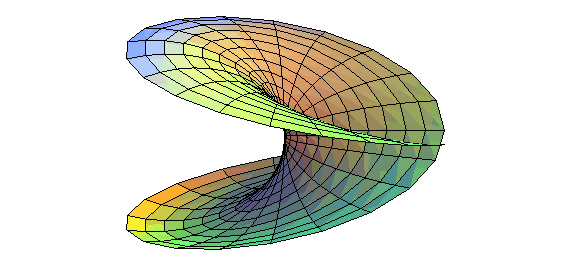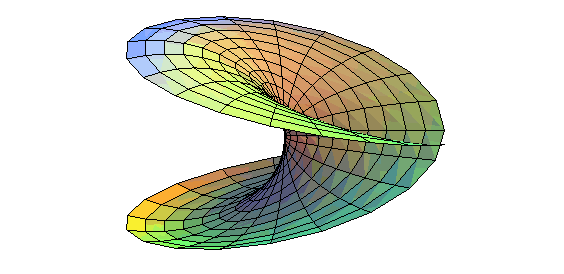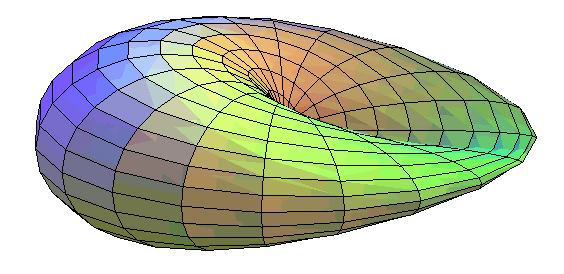
| Cartesian parametrization of Apery (1986), used for the
images above:
Cartesian parametrization of Bryant-Kusner (1987): Cartesian parametrization of Morin-Apery (1987), ranging from the Roman surface (k = 0) to Boy's surface (k = 1): Algebraic surface of degree 6. |
Boy's surface was discovered after the search of a model
in of
the projective plane that
would not have other singularities than self-intersections along which
the various surfaces would have a well-defined tangent plane (the Roman
surface and the cross-cap,
which were known, have cuspidal points).
Boy described his surface in a conceptual way, and it
is only in 1981 that J.P.
Petit and J. Souriau found a parametrization of it.
| Much as the cross-cap is obtained by twisting the edge of a disk into a curve with one crossing until the two parts coincide (so that the opposite points of the disk coincide)... |  |
 |
| ...Boy's surface is obtained by twisting a disk into a curve with three crossings until the 6 parts coincide two by two (hence the order 3 symmetry of this surface) |  |
 |
| Opposite, various animations explaining the construction (Bryant-Kusner parametrization): |  |
 |
 |
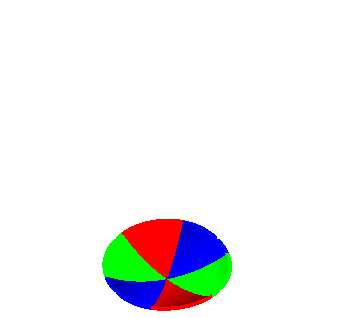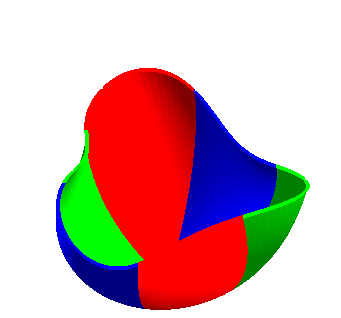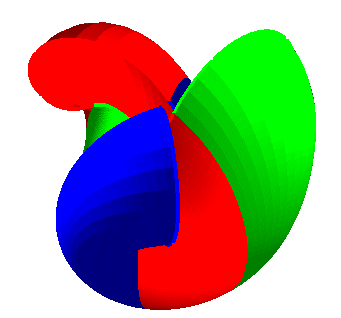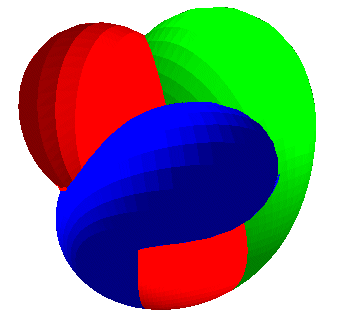
| Boy's surface has 3 orifices leading to tunnels that
come together in the central part.
Follow a path to understand that the surface has only one face. |
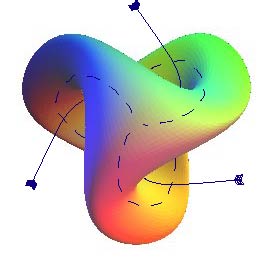 |
| Opposite, an animation using the Morin-Apery parametrization,
showing the deformation of the Roman
surface into Boy's surface; the 3 cuspidal points of the Roman surface
disappear as from |
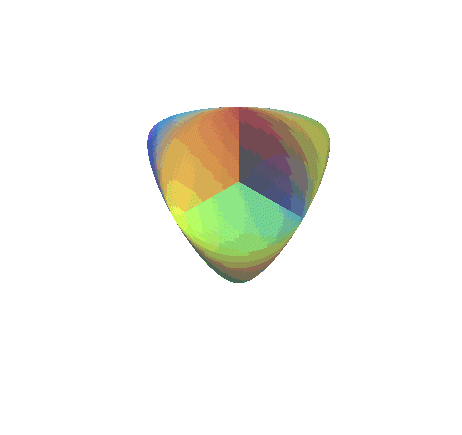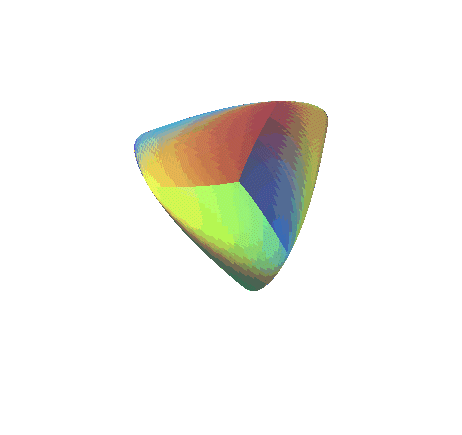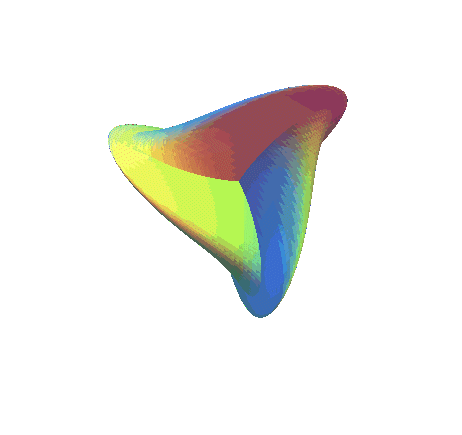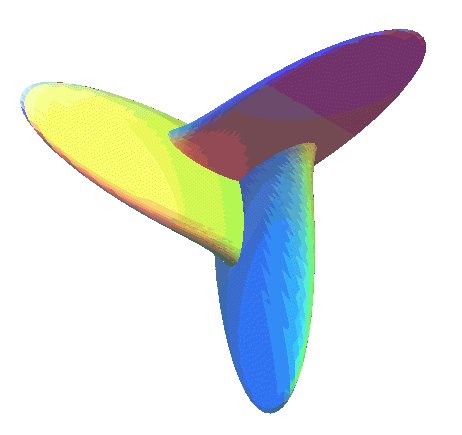 |
| The self-intersection curve of Boy's surface is a twisted
trifolium; the
3 tangents at the triple points are orthogonal two by two (and therefore
so are the three tangent planes of the surface at this triple point).
See also quadrifolium. |
 |
 |
The above parametrization of Morin-Apery makes it an algebraic
surface of degree 6, and it has been proved that this degree could not
be lowered without cuspidal points appearing (the Roman surface and the
cross-cap are quartics).
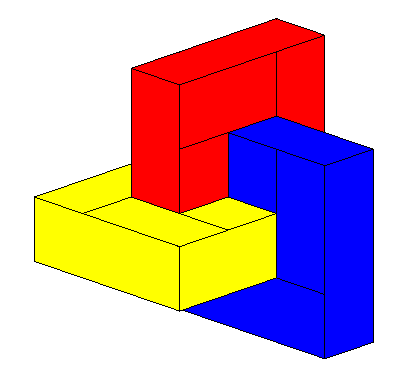
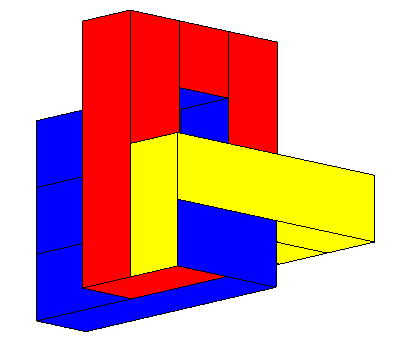
| Here is a model of Boy's surface in the form of a reunion
of linked rectangles.
The self-intersection curve is composed of 3 squares located in 3 planes two by two perpendicular to one another. Since some adjacent rectangles are coplanar, this model should be deformed to truly become a polyhedron, but there exists a true (generalized) polyhedron that is a model for Boy's surface: Brehm's polyhedron. |
  |
If Boy's surface is painted, the layer of paint obtained
(which is in one piece since this surface is one-sided) is an immersion
of the sphere (because the two-sheeted
covering space of the projective plane is the sphere); it is the reason
why Boy's surface was used as the central step in the process of turning
a sphere inside out: see for example this
text in Pour la Science.
See also the Morin surface.

| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017